一种结构动力学系统逆向建模的可解释神经网络及方法
文献发布时间:2024-04-18 19:58:21
技术领域
本发明涉及人工智能领域与结构动力学领域,尤其涉及一种用于结构动力学系统逆向建模的可解释神经网络及方法。
背景技术
目前,可解释人工智能的研究得到了世界各强国的高度重视。在2015年,美国国防部高级研究计算局(DARPA)制定了可解释人工智能(XAI)计划,其目标是使最终用户能够更好地理解和信任人工智能系统学习到的模型和决策;2022年6月3日,美国国防部高级研究计算局(DARPA)宣布推出最新的人工智能(AI)项目——“有保证的神经符号学习和推理”(ANSR),试图以新的、混合的(神经符号)AI算法的形式来解决诸多挑战,该算法将符号推理与数据驱动深度融合,以创建强大的、运算有逻辑规则支撑而值得信赖的人工智能系统。同时,我国也于2021年提出了“可解释、可通用的下一代人工智能方法”重大研究计划,并在2022年与2023年连续发布研究指南,旨在号召我国科研人员积极开展相关研究,以打破现有深度学习“黑箱算法”的现状,建立一套可适用于不同领域、不同场景的通用方法体系。可见,可解释人工智能的研究,是未来人工智能领域需要突破的重要方向;开展可解释人工智能的研究并应用于航空航天等领域的难点问题解决,正是上述研究方向提出的重要背景组成。而结构动力学系统的逆向建模作为结构动力学研究领域反问题的研究基础,正是亟需此类先进技术支撑的关键难点问题之一。
结构动力学系统的建模分为正向建模与逆向建模两种。正向建模用于对实际结构建立正向的理论模型或数值仿真模型,以解决结构动力学领域的正问题——精确计算实际结构在动载荷作用下产生的动响应;逆向建模则主要用于模型辨识及建立实际结构的逆模型,并由此解决结构动力学领域的反问题——结构动力学参数辨识问题以及结构动载荷识别问题。
结构的正向动力学建模技术较为成熟,包括理论建模技术、有限元建模技术、传递矩阵法建模技术、机器学习技术等;而结构动力学逆向建模方法与技术手段十分有限,且均存在各自的缺陷。现有的方法主要有正模型求逆法、统计与估计方法及机器学习方法三类。正模型求逆法主要包括频响函数矩阵直接求逆法、正则化方法等,是基于精确的结构动力学正向模型进行求逆运算,进而获得逆向的结构动力学模型;统计与估计方法主要包括卡尔曼滤波方法、贝叶斯估计方法等,是在相对精确的结构动力学正模型基础上,采用统计与概率估计的方法,进一步地完成参数估计,对存在部分参数不确定的情况有适用性;机器学习方法主要依赖于现有的黑箱式人工神经网络模型如LSTM神经网络、卷积神经网络等等,通过采用数据驱动的手段,建立用于映射结构动力学逆向关系的代理模型。正模型求逆法和统计与估计方法可统称为传统数学方法;机器学习方法则主要依赖于人工神经网络建模方法。
面向航空结构工程领域中,应用人工神经网络进行动载荷识别难点问题解决,无疑具有更广阔的应用前景和更深的潜力。但本申请发明人在实现本申请实施例中发明技术方案的过程中,发现上述现有技术至少存在如下技术问题:
基于传统数学推理的结构动力学系统逆向建模方法是基于数学推理所建立的,具有原理性强、物理意义明确的特点;但也由于其必须基于受载结构的精确数学模型,且其中不可避免的矩阵求逆运算,往往容易出现计算困难、不适定等一系列问题,造成了这类方法具有先天的局限性,无法再得到进一步的突破性提升。而基于人工神经网络的结构动力学系统逆向建模方法可以不必像传统方法那样建立振动响应与动载荷之间的理论表达式,而是利用深度神经网络对于结构动力学系统逆向建模问题进行代理模型的建立,充分发挥深度神经网络对于强相关关系的拟合能力,由此避免了如高精度数学理论建模、理论模型误差控制等诸多困难;但目前此类建模方法都聚焦于人工神经网络在结构动力学系统逆向建模问题中的应用方法尝试与验证,而现有技术手段都没有关注于结构动力学理论与机器学习方法在底层上的真正融合,即没有使人工神经网络模型在物理意义上具备可解释的计算架构。也就是说,目前应用于结构动力学系统建模的深度神经网络模型在运行机制上都缺乏力学机理角度的可解释性,因此,人工神经网络模型在工程实际中的泛化性是无法从根本上保证的。继而在面向实际工程应用时,人工神经网络模型的鲁棒性等关键问题也难以解决。而这也直接造成了现有的结构动力学系统逆向建模方法大多只能停留于提出方法设想与初步验证其可行性的阶段,难以进一步纵深挖掘问题和方法背后的科学机理,同时也难以推动现有研究成果真正走向工程实际。而“人工神经网络模型的可解释性”也至此成为学界和工程界都最为关注和亟需突破的关键壁垒。
发明内容
针对现有应用于动载荷识别领域的深度神经网络不具备物理意义上的可解释、模型鲁棒性与泛化性不足、对数据样本过度依赖等模型固有缺陷,本发明设计出可以对结构动力学逆向物理关系进行全解析式映射的可解释神经网络,揭示基于物理知识构架的可解释神经网络泛化机理,最终建立起一套适用的、基于可解释神经网络的结构动力学系统逆向建模方法。
本发明的技术方案为:
一种结构动力学系统逆向建模的可解释神经网络,包括输入层、隐含层和输出层;
其中输入层、隐含层和输出层中,每层的神经元个数取采集的结构动力学系统动响应自由度个数p;
所述输入层中第i个神经元的输入信号为结构动力学系统动响应[x
所述输出层中第i个神经元的输入信号为构造的中间变量
所述隐含层中的第i个神经元的输入信号第i阶模态动响应y
而对于上述可解释神经网络的训练方法,包括以下步骤:
步骤1:物理参数神经网络预训练:
步骤1.1:根据结构的边界条件与外形尺寸计算结构模态振型矩阵[φ],并给出结构的模态质量、模态阻尼与模态刚度初始值;
步骤1.2:根据结构模态振型矩阵[φ]计算[φ]
步骤2:准备训练数据:
采集受载结构的动响应时域数据样本X(t)与动载荷时域数据样本F(t);
结合结构模态振型矩阵[φ],利用采集的动响应时域数据样本X(t)与动载荷时域数据样本F(t),得到隐含层的输入信号:模态动响应时域信号y(t),以及隐含层的输出信号:频域内的虚拟模态动载荷
采用隐含层的输入数据与输出数据作为训练数据样本;
步骤3:利用训练数据对所述神经网络进行训练,得到结构的模态质量、模态阻尼与模态刚度结果;
其中对于隐含层的第i个神经元的输出
可以看出,本发明首先设计提出一种在物理意义上具有完全可解释性的神经网络模型结构,通过将具有力学机理的结构动力学系统逆向计算关系进行神经网络化,依据其计算流程设计神经网络的整体计算架构与神经元模块,并将物理参数嵌入神经元内部,使其具有明确的建模规则和完全可解释性,解决了现有技术中人工神经网络计算流程不透明、网络参数不具备物理涵义的瓶颈。进一步地,通过设计上述可解释神经网络的专有训练方法,解决传统的结构动力学系统逆向建模方法中计算困难、矩阵病态、求解不适定等一系列问题,以及现有的人工神经网络在运行机制与模型机理上缺乏可解释性,继而过度依赖于训练样本、缺乏泛化性及鲁棒性等问题,实现了基于数据与知识双驱动的手段对结构动力学系统实现精确、直接的逆向建模,具有优越的泛化能力、计算精度和计算效率,并具备结构动力学反问题解决的能力。
有益效果
本发明具有如下技术效果或优点:
1、由于采用了将结构动力学系统逆向计算关系进行神经网络化设计,所以本发明有效解决了现有应用于结构动力学系统建模的人工神经网络不具备力学机理上可解释的计算流程、模型泛化性不足的问题,进而实现了能够采用可解释神经网络架构对结构动力学系统进行符合动力学规律运算的逆向建模。
2、由于采用了将结构动力学参数融入神经元内部,所以,有效解决了现有应用于结构动力学系统建模的人工神经网络内部神经元参数不具备物理含义的问题,进而实现了能够让可解释神经网络的内部参数能够对结构动力学参数进行解析式映射。
3、由于采用了专用于可解释神经网络的训练方法,所以,有效解决了现有应用于结构动力学系统建模的人工神经网络训练过程过度依赖于样本数据集、难以保证神经网络正确训练的问题,进而实现了能够让可解释神经网络基于小规模的样本数据集,通过数据驱动的方法实现快速、正确的训练。
本发明的附加方面和优点将在下面的描述中部分给出,部分将从下面的描述中变得明显,或通过本发明的实践了解到。
附图说明
本发明的上述和/或附加的方面和优点从结合下面附图对实施例的描述中将变得明显和容易理解,其中:
图1为输入层及输出层端部物理参数神经元示意图;(a)输入层物理参数神经元,(b)输出层物理参数神经元;
图2为内部物理参数神经元示意图;
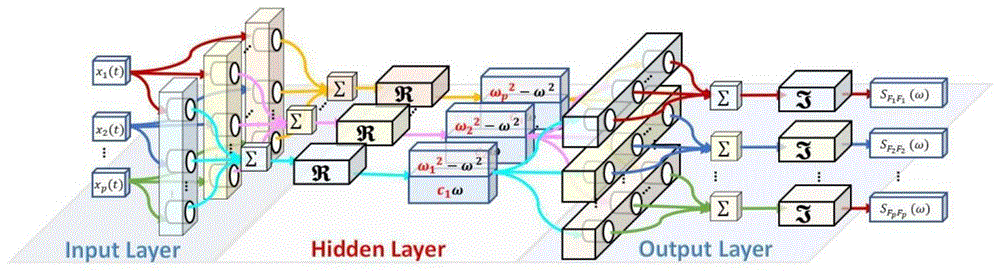
图3为可解释物理参数神经网络示意图;
图4为本申请实施例1中八自由度离散振动系统示意图;
图5为本申请实施例1中各神经元参数的收敛过程示意图;(a)模态刚度参数k′
具体实施方式
解决现有应用于结构动力学系统建模的人工神经网络模型不具备物理意义上可解释性、泛化性难以保证的核心技术问题,本发明采用结构动力学方程作为可解释的符号网络式计算架构,将结构动力学参数嵌入至所构建的神经网络内部,从而设计实现了一款物理参数嵌入的、具有物理意义上完全可解释性的神经网络模型,称为IPENN(可解释物理嵌入式神经网络,Interpretable Physic-Embedded Neural Network);在此基础上,进一步设计了IPENN的训练方法,并基于此提出一套可以利用数据驱动手段实现对结构动力学系统进行全解析式的逆向直接建模方法。
步骤1、构建可解释物理参数神经网络
(1.1)构建结构动力学系统的频域逆向动力学关系
任意的线性时不变结构动力学系统均可等效为多自由度离散振动系统进行动力学建模。对于一个n自由度的离散振动系统,依据模态分析理论,作用于其上的动载荷F及其产生的动响应X,可分别表示为n阶模态动载荷f与模态动响应y的叠加。由于实际结构是连续的,理论上的n往往需要趋近于无穷;而F(ω)的频率范围是有限的,通常高阶的模态动载荷与模态动响应的占比很小,可以忽略,因此可以进行合理的模态截断。
对于n自由度离散振动系统,假设其共受到q个动载荷的作用,即F=[F
其中,φ
其中,
(1.2)多自由度离散振动系统的频域逆向动力学计算关系拓展
由式(2)可知,第i阶模态下,f
f
进一步地,可将式(5.a)推广至式(5.b):
其中,
则
同时,
为F
至此,结合上述式(1)-式(9),重新梳理从X(t)到S
①y(t)=[φ]
②
③
④
⑤
基于式(10.a)-(10.e),进行可解释神经元与人工神经网络的设计。
(1.3)物理参数神经元与可解释物理参数神经网络设计
依照式(10.a)与式(10.d),设计端部物理参数神经元,作为物理参数神经网络的输入层与输出层的基本组成单元;其计算结构如图1所示。与传统的人工神经元类似,端部物理参数神经元同样通过接收外界输入信号[x
依照式(7),设计内部物理参数神经元,作为物理参数神经网络的隐含层的基本组成单元;其计算结构如图2所示。对于第i个内部物理参数神经元,其权重向量为[m
基于上述设计得到的物理参数神经元,构建可解释物理参数神经网络如图3所示。神经网络的输入信号为动响应时域信号X(t),输出信号为动载荷的功率谱密度S
步骤2、建立可解释物理参数神经网络训练方法
(2.1)物理参数神经网络预训练
物理参数神经网络的预训练方法,是基于人工先验知识,完成物理参数神经网络的初始化参数设置。在工程实际中,结构的边界条件与外形尺寸是容易精确可知的;而结构所使用材料的密度、弹性模量及阻尼等参数往往难以直接测量获取。反映在结构动力学模型中,结构的模态振型矩阵[φ]可以依据结构的边界条件与外形尺寸精确计算得到;而结构的模态质量m
因此,可以依据人工先验知识,计算得到精确的[φ],与初始的m
(2.2)训练数据准备
由2.1节易知,物理参数神经网络的待训练物理参数均集中于物理参数神经网络的隐含层,所以,本发明直接采用隐含层的输入数据与输出数据作为训练数据样本,对物理参数神经网络的隐含层进行训练。因此,需要按照物理参数隐含层的输入信号与输出信号准备训练样本数据集。
首先,采集受载结构的动响应时域数据样本X(t)与动载荷时域数据样本F(t);之后,由于隐含层的输入信号为模态动响应时域信号y(t),输出数据为频域内的虚拟模态动载荷
(2.3)物理参数神经网络训练算法
对于隐含层的第i个神经元的输出
其中
显然,
在物理参数神经网络的训练过程中,首先基于
综上所述,针对具体的结构动力学系统,进行基于可解释物理参数神经网络的结构动力学系统逆向建模的过程为:
针对具体的结构动力学系统,依据上述可解释神经网络模型构建方法,构建与之对应的可解释神经网络基础模型;
依据上述要求,采集加载于结构的动载荷与动响应信息,并进行数据处理,完成可解释神经网络的训练数据集准备;
之后,依据上述的可解释神经网络训练方法,首先依据先验物理知识,进行可解释神经网络的预训练;然后采用准备好的训练数据,借助本发明所设计的训练算法,对可解释神经网络进行数据驱动式训练,从而最终完成可解释神经网络对结构动力学系统的逆向建模。
为了更好的理解上述技术方案,下面将结合说明书附图以及具体的实施例对上述技术方案进行详细的说明。
本实施例采用如图4所示的8自由度离散振动系统,检验可解释物理参数神经网络的动载荷识别能力。8自由度离散振动系统的弹簧的刚度参数为K
现假设上述参数均为未知。设定刚度参数初始值K′
之后,将一段频带宽度为0-50Hz,幅值为200N,时长为30s的正弦扫频式动载荷信号样本加载于端部集中质量,并采集各个集中质量的动响应信号样本,再依照前文的数据处理方法进行数据处理,作为训练样本数据集。
此外,将一段频带宽度为0-50Hz,时长为30s的平稳随机动载荷信号样本加载于端部集中质量,并采集各个集中质量的动响应信号样本,再依照前文的数据处理方法进行数据处理,作为随机动载荷测试样本数据集。
将一个峰值为1000N,脉宽为0.02秒的三角波冲击载荷信号样本加载于端部集中质量,并采集各个集中质量的动响应信号样本,再依照前文的数据处理方法进行数据处理,作为冲击载荷测试样本数据集。
依照前文的训练方法进行可解释物理参数神经网络的训练。设置初始学习率参数为0.1,训练迭代步数为300步;仅采用AMD Ryzen 9 5950X型CPU完成训练(无GPU加速),训练总时长仅为2.85s。整个训练过程中,各神经元参数的收敛过程如图5所示。
在可解释物理参数神经网络完成训练后,基于神经元参数k′
表1ω
表2ξ
注:表中0.00%的相对误差是由于数据误差过小,在位数截断后的舍入误差达到0.00%;而非绝对误差为0.00%。
由表中对比结果可以得到,模态参数的辨识结果非常精确,固有频率参数的最大误差不超过0.05%,模态阻尼比的最大误差不超过1%。
可以看到,采用可解释神经网络实现了对此8自由度的动力学系统实现了精准的、全解析式的逆向建模。
可解释物理嵌入式神经网络(IPENN)将物理参数嵌入神经元内部,具有明确的建模规则和完全可解释性。IPENN通过引入物理意义和解释性克服了现有基于人工神经网络的动载荷识别方法的局限性,为动载荷识别提供了一种强大的工具,并且展现出优越的泛化能力、计算精度和计算效率。此外,它成功地将动载荷识别与模态参数辨识的功能结合起来,对于结构动力学领域的反问题解决具有广泛的适用性。因此,本发明为结构动力学建模领域与结构动力学反问题领域提供了一种新颖且可解释的方法,推动了结构动力学的理论认识和实际应用的发展。
尽管上面已经示出和描述了本发明的实施例,可以理解的是,上述实施例是示例性的,不能理解为对本发明的限制,本领域的普通技术人员在不脱离本发明的原理和宗旨的情况下在本发明的范围内可以对上述实施例进行变化、修改、替换和变型。
- 一种基于动力学及深度神经网络的进给系统混合建模方法
- 一种基于动力学及深度神经网络的进给系统混合建模方法
