一种基于改进A星算法的车辆导航方法

技术领域

本发明涉及路径规划技术领域，特别是涉及一种基于改进A星算法的车辆导航方法。

背景技术

自动导引运输车(Automated Guided Vehicle，AGV)是指装备有电磁或光学等自动导引装置，它能够沿规定的导引路径行驶，具有安全保护以及各种移载功能的运输车。AGV系统的控制是通过物流上位调度系统、AGV地面控制系统及AGV车载控制系统三者之间的相互协作完成的。

在对AGV小车进行导航控制时，使用传统的A*算法在求解路径规划时会存在以下两个突出缺点：

(1)传统A*算法规划出的路径会出现较多的转折点，折点过多对于现实中AGV的运行会造成不利的影响，过多的转向意味着造成更多的时耗。

(2)传统A*算法在搜索路径时会拓展过多的节点，造成了计算的耗时和资源的浪费。

发明内容

本发明的目的是提供一种基于改进A星算法的车辆导航方法，降低转向消耗，提高了导航效率。

为实现上述目的，本发明提供了如下方案：

一种基于改进A星算法的车辆导航方法，包括：

将待规划路径的区域地图转换为栅格地图；

采用改进的A*算法在所述栅格地图上规划出自动导引运输车从起点到目标点的目标行驶路径；所述改进的A*算法为将转向消耗成本引入代价函数后的A*算法；

采用所述目标行驶路径为所述自动导引运输车导航。

可选地，采用改进的A*算法在所述栅格地图上规划出自动导引运输车从起点到目标点的目标行驶路径，具体包括：

为起点初始化一个父节点，将起点的父节点传入Open集合；

将Open集合中代价函数值最小的节点移出，移入Close集合，并将该移动代价最小的节点作为当前节点；

为当前节点扩展邻居节点；

遍历当前节点扩展的邻居节点，若当前遍历到的邻居节点不在Close集合中，则根据当前节点、当前节点的父节点和当前遍历到的邻居节点判断当前节点是否为转向节点；

若当前节点是转向节点，则采用引入了所述转向消耗成本的代价函数重新计算当前节点到当前遍历到的邻居节点的代价函数值；当前计算的代价函数值包括移动代价和预计代价；

若重新计算后的移动代价小于重新计算前的移动代价，则将重新计算后的代价函数值更新为当前节点的代价函数值，并将当前节点更新为当前遍历到的邻居节点的父节点，将当前遍历到的邻居节点存入Open集合；

返回将Open集合中代价函数值最小的节点移出，移入Close集合，并将该移动代价最小的节点作为当前节点的步骤，直到当前节点扩展的邻居节点包括目标点，改进的A*算法结束。

可选地，引入了所述转向消耗成本的代价函数表示为：

f(n)＝g(n)+h(n)；

g(n)＝step_cost(n)+turn_cost(n)；

其中，f(n)为节点n的代价函数值，g(n)为节点n的移动代价，h(n)为节点n距离终点的预计代价，step_cost(n)为节点n直线移动的代价，turn_cost(n)为节点n的转向消耗成本。

可选地，根据当前节点、当前节点的父节点和当前遍历到的邻居节点判断当前节点是否为转向节点，具体包括：

若当前节点的父节点的横坐标和当前节点的横坐标相同，且当前节点的横坐标和当前遍历到的邻居节点的横坐标不相同，则当前节点为转向节点；

若当前节点的父节点的纵坐标和当前节点的纵坐标相同，且当前节点的纵坐标和当前遍历到的邻居节点的纵坐标不相同，则当前节点为转向节点。

可选地，所述转向消耗成本设置为0.01。

可选地，所述改进的A*算法中代价函数还表示为：

f(n)＝g(n)+w*h(n)；

其中，f(n)为节点n的代价函数值，g(n)为节点n的移动代价，h(n)为节点n距离终点的预计代价，w为动态参数。

可选地，若节点n与所述目标点的距离大于设置距离，则w＝1.5，否则w＝0.95。

根据本发明提供的具体实施例，本发明公开了以下技术效果：

本发明改进的A*算法中计算移动代价时将转向消耗成本引入代价函数，降低了路径规划中转折点的数量，降低了AGV小车转向的频次，从而降低转向消耗，进而提高了导航效率。

附图说明

为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动性的前提下，还可以根据这些附图获得其他的附图。

图1为本发明实施例提供的一种基于改进A星算法的车辆导航方法；

图2为本发明实施例提供的A星算法的流程图；

图3为本发明实施例提供的32*32的栅格地图；

图4为本发明实施例提供的传统A星算法生成的路径示意图一；

图5为本发明实施例提供的传统A星生成的路径存在折点过多的问题以及期望改进的减少折点的效果示意图；

图6为本发明实施例提供的节点n和节点n-1、节点n+1的三点坐标的位置关系示意图；

图7为本发明实施例提供的转向消耗成本turn_cost＝0.5的改进A星算法生成路径效果示意图；

图8为本发明实施例提供的不同转向消耗成本的路径规划的效果示意图；

图9为本发明实施例提供的小规模地图中改进前后的A星算法生成的路径对比示意图；

图10为本发明实施例提供的传统A星算法生成的路径示意图二；

图11为本发明实施例提供的改进A星算法生成的路径示意图；

图12为本发明实施例提供的32*32栅格尺寸下A星算法规划路径的扩展节点示意图；

图13为本发明实施例提供的50*50栅格尺寸未优化启发函数的扩展节点示意图；

图14为本发明实施例提供的50*50栅格尺寸启发函数权重为2的扩展节点示意图；

图15为本发明实施例提供的50*50栅格尺寸启发函数权重为4的扩展节点示意图；

图16为本发明实施例提供的随机生成地图，权重为1的示意图；

图17为本发明实施例提供的随机生成地图，权重为1.5的示意图；

图18为本发明实施例提供的随机生成地图，权重为3的示意图。

具体实施方式

下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

本发明的目的是提供一种基于改进A星算法的车辆导航方法，降低转向消耗，提高了导航效率。

为使本发明的上述目的、特征和优点能够更加明显易懂，下面结合附图和具体实施方式对本发明作进一步详细的说明。

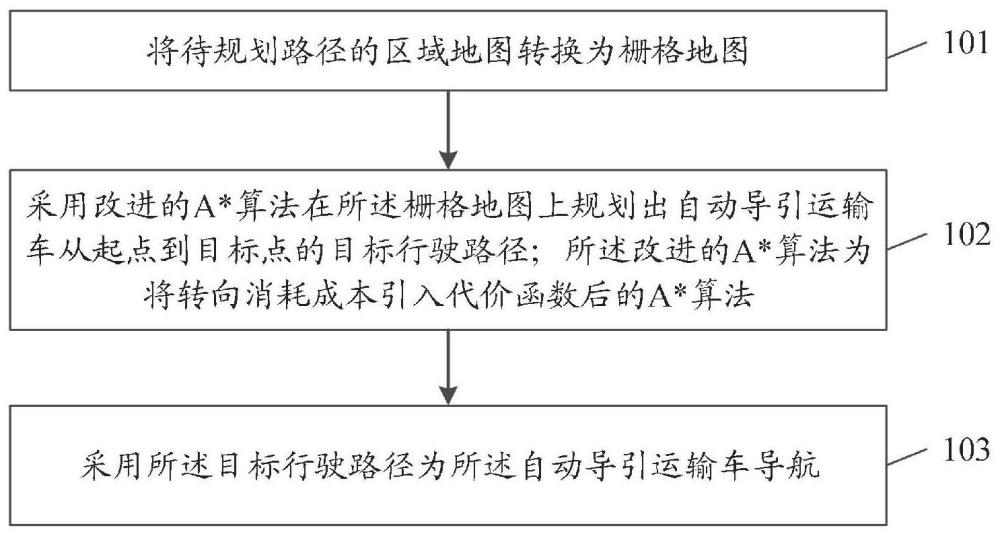
如图1所示，本发明提供了一种基于改进A星算法的车辆导航方法，该方法具体包括如下步骤。

步骤101：将待规划路径的区域地图转换为栅格地图。

步骤102：采用改进的A*算法在所述栅格地图上规划出自动导引运输车从起点到目标点的目标行驶路径；所述改进的A*算法为将转向消耗成本引入代价函数后的A*算法。

步骤103：采用所述目标行驶路径为所述自动导引运输车导航。

传统A星(A*)算法原理如下。

A*(A-STAR)算法同时使用了从起点开始的实际距离和距离目标点的预估距离作为代价函数，很大地改善了Dijkstra算法在搜索到目标点之前探索过多的无用节点造成时间浪费的缺点，和贪婪算法经常找不到最优路径的缺点，但是会优先考虑可能更接近目标的路径，是一种适应性强灵活性更高的启发式路径规划搜索算法，被常应用移动机器人的全局路径规划问题中。

A*算法靠引入启发函数和结合代价函数来对扩展的节点进行评估，代价函数表示为：

f(n)＝g(n)+h(n)。

A*算法的流程和Dijkstra算法流程类似，不同点在迭代过程中引入代价函数f(n)并基于此来选取最小代价值的点，程序中常引用两个列表Close列表和Open列表，原理上映射为上文Dijkstra算法中介绍的S集合和U集合，一个用来存放已经扩展的当前节点和障碍物节点以防止后续扩展到里面的节点，一个用作存放待扩展的节点，在算法中常创建名为Close和名为Open的列表或者集合。

f(n)是节点n的综合优先级。当选择下一个要遍历的节点时，总会选取综合优先级最高(值最小)的节点。

g(n)是节点n距离起点的代价。

h(n)是节点n距离终点的预计代价，这也就是A*算法的启发函数。

如图2所示，A*算法搜索路径的工作步骤如下：

1.把起点加入Open列表。

2.重复如下过程：

a.遍历Open列表，查找f(n)值最小的节点，把它作为当前节点。

b.把这个节点移到Close列表。

c.对当前方格相邻方格进行遍历：

如果相邻方格的点不可抵达或在Close列表中，将对它进行跳过；

如果它不在Open列表中，把它加入Open列表，并且把当前方格设置为它的父节点，记录该方格的f(n)，g(n)和h(n)值；

如果它已经在Open列表中，计算经由当前方格到达它那里的消耗g(n)是否更小。更小则表示是条更短更优的路径。此时将当前方格更新为它的父节点，并重新计算它的g(n)和f(n)值，即更新它的信息；

d.当终点被加到Open列表中或Open列表为空，算法停止。

3.保存路径。从终点开始，每个方格沿着父节点移动直至起点，得到路径。

图2中O表表示Open列表，C表表示Close列表。

在操作系统Windows10，编程环境Python3.8的环境下，设计了基于应用原始A*算法在AGV的路径规划问题进行求解，使用Plot库的工具对输出的数据进行可视化的仿真实验。仿真的地图环境设计为32*32的栅格地图，障碍物为随机生成，路径规划仿真结果如图4所示，其中的黑色方格表示障碍物区域，机器人不可通行；空白方格表示可通行的无障碍区，AGV只能够在可通行区域移动行走；从起点到目标点的线条表示规划的路径，图4中圆圈表示起点。

图4中，左下角坐标为(1,1)的圆点代表AGV，右上角坐标为(31,31)的方块表示AGV的目标点，从起点到目标点的线为规划出来的线路，本次代码的路径规划求解部分运行时间为0.5026683s，折点数量为22，行走消耗代价为61，扩展节点数为432。

通过仿真结果可以得出原始的A*算法应用在路规划求解问题中可以迅速绕开障碍物顺利找到最终目标点的结论。但是从显示的生成路径以及搜索中扩展的节点数上发现两点不足：

1)传统A*算法应用在AGV的路径规划时，求解得到的路径并不能称作是比较好的，原因是规划出的路径中存在着转折点数过多、路径不够平滑等问题，现实中的机器人如果沿着这条折线移动会造成频繁的转向，造成过多的运动损耗。

2)在搜索中扩展的节点数过多，打印的扩展节点显示在搜索过程中搜索了过多的无用的节点，最终导致了搜索效率的下降。

为了得到更加符合AGV实际运行中的成本代价，并使得路径更加平滑。提出了一种基于坐标点判断是否发生转折的方法，实际消耗函数g(n)将由实际移动距离step_cost(n)和转向消耗函数turn_cost(n)共同组成，其中step_cost(n)代表实际的移动成本，移动一次的成本记为1*step_cost，turn_cost(n)代表转向消耗成本，如果发生一次转向则增加一次转向消耗成本turn_cost，则图5中A*算法的路径规划的实际消耗函数g(n)表示为：

g(n)＝step_cost(n)；

改进的A*算法的路径规划的实际消耗函数g(n)表示为：

g(n)＝step_cost(n)+turn_cost(n)；

由改进前后的实际消耗函数可以预知，A*算法在扩展搜索节点时在转向代价函数的影响下将会根据路径的消耗选择出一条折点数更少的路径，图5中(a)原始A*算法的路径成本为8次移动加3次转向，而图5中(b)改进A*算法的路径成本为8次移动加2次转向，消耗更小。

为了区分设计不同移动状态下的消耗成本g(n)的设计，需要能够判断在规划的路径时是否出现了折点，根据判断是否是转折点来更改代价函数。

将AGV运动的时空信息表示在栅格图中，n时刻AGV所处的坐标点用(x

利用连续的三个点的前两个点的位置关系信息就可以判断出第三个点是不是转向后移动的点，由于点(x

x

如果是x

以上的分析是从机器人前两个位置的坐标值来判断第三个点是不是转折后的移动的点。

其中，步骤101中将待规划路径的区域地图转换为栅格地图具体包括：将机器人的实际工作环境切割为一个个单位栅格大小的形状，把真实的环境信息转换为抽象的数据信息，不同的栅格点可以用来分别表示真实环境中的可通行区域、起点、目标点、障碍物点等各种点。栅格法正是因为其具有数据处理相对简单、易于维护、刻画信息直观且相对丰富，便于观察等诸多优点。在机器人理解的工作环境下根据机器人能够在栅格点内移动的栅格和显示中对应的障碍物不可通行的栅格分为可自由通行栅格与障碍物栅格。设置栅格颜色时，可以将栅格地图中呈现为黑色的栅格用来描绘机器人工作的环境，白色的栅格用以描绘机器人的可通行区域，如图3所示。

算法在Open集合不为空时将会从集合中选择f(n)最小的节点作为当前点(current)然后从当前点的四邻域展开拓展搜索，改进后的算法需要在拓展节点时增加一步折点判断的函数，在此基础上设定转向代价。算法中通过判断当前点的坐标x和y的值和当前点的父节点坐标的x和y的值进行判断，以前一步判断的结果结合当前点和扩展点坐标值进行判断且二者的判断结果必须同时满足设定的条件才算做一次转弯，由于第一个点起始点是没有父节点的，因此需要为起始点预设一个父节点，否则程序将无法运行。

其中，步骤102具体包括：

为起点初始化一个父节点，设置转向惩罚成本，将起点的父节点传入Open集合，初始移动代价为0。

将Open集合中代价函数值最小的节点移出，移入Close集合，并将该移动代价最小的节点作为当前节点。

为当前节点扩展四个方向的邻居节点。

遍历当前节点扩展的邻居节点，若当前遍历到的邻居节点不在Close集合中(若在，则跳过)，则根据当前节点、当前节点的父节点和当前遍历到的邻居节点判断当前节点是否为转向节点。

若当前节点是转向节点，则采用引入了所述转向消耗成本的代价函数重新计算当前节点到当前遍历到的邻居节点的代价函数值。当前节点的代价函数值f(n)包括移动代价g(n)和预计代价h(n)。

若重新计算后的移动代价小于重新计算前的移动代价，则将重新计算后的代价函数值更新为当前节点的代价函数值，并将当前节点更新为当前遍历到的邻居节点的父节点，将当前遍历到的邻居节点存入Open集合，否者跳过。

返回将Open集合中代价函数值最小的节点移出，移入Close集合，并将该移动代价最小的节点作为当前节点的步骤，直到当前节点扩展的邻居节点包括目标点，改进的A*算法结束。

本发明中，若当前节点的父节点的横坐标和当前节点的横坐标相同，且当前节点的横坐标和当前遍历到的邻居节点的横坐标不相同，则当前节点为转向节点；若当前节点的父节点的纵坐标和当前节点的纵坐标相同，且当前节点的纵坐标和当前遍历到的邻居节点的纵坐标不相同，则当前节点为转向节点。

本发明引入了所述转向消耗成本的代价函数表示为：

f(n)＝g(n)+h(n)；

g(n)＝step_cost(n)+turn_cost(n)；

其中，f(n)为节点n的代价函数值，g(n)为节点n距离起点的代价(移动代价)，h(n)为节点n距离终点的预计代价，step_cost(n)为节点n直线移动的代价，turn_cost(n)为节点n的转向消耗成本，若节点n不是转向节点，则g(n)＝step_cost(n)。

转向消耗成本函数伪代码如表1所示。

表1折点优化方法伪代码

表1中，a表示转向消耗成本初始值，neighbor表示邻居节点，neighbor_list表示邻居节点集合，close_set表示Close集合，current.x表示当前节点的x轴坐标，came_from[current].x表示当前节点的父节点的x轴坐标，neighbor.x表示邻居节点的x轴坐标，current.y表示当前节点的y轴坐标，came_from[current].y表示当前节点的父节点的y轴坐标，neighbor.y表示邻居节点的y轴坐标，g为更新过后的移动代价，current.g表示当前的移动代价，step_cost即为step_cost(n)，turn_cost即为turn_cost(n)，open_set表示Open集合，neighbor.f表示邻居节点的代价函数值，neighbor.g表示邻居节点的移动代价，neighbor.h表示邻居节点的预计代价。

对设计了转向惩罚函数后的改进A*算法进行多次仿真验证，为验证设置的转向惩罚成本大小对最终规划路径的影响，通过设置不同大小的转向惩罚成本进行对比仿真实验，对比了不同的转向成本对路径折点及最终长度的影响。图7为32*32地图中转向惩罚设置为turn_cost＝0.5时的路径规划。

图8为转向惩罚成本分别设置为0.01、0.05、0.2、0.5、0.7时在同一张地图中的路径规划信息，主要记录了最短路径的距离、路径中出现的折点数、以及搜索的扩展节点数。

经过多次不同转向惩罚成本(转向消耗成本)的仿真实验对比，实验结果数据表明：转向代价turn_cost在选取一个较小的值如0.01、0.05时规划的路径折点数最少、扩展的节点相近且规划的路径时最短的；当设置一个相对大的值如0.2、0.5、0.7时，规划出的路径将分别会出现扩展节点增多、折点数增多以及规划的路径不是最短路径的缺陷现象。综合考虑将以下仿真实验的转向惩罚成本设置为turn_cost＝0.01。

图9展示了简单环境下的原始A*算法和改进的A*算法(图9中(b))的路径规划效果，图9中(a)为原始A*算法路径规划效果，图9中(b)为改进的A*算法路径规划效果。

A*算法改进前和改进后在8*8地图中搜索路径的信息对比如表2所示。

表2优化前后的A*算法对比

图10展现了32*32尺寸的复杂环境的传统A*算法的路径规划效果图，图11展现了32*32尺寸的复杂环境的改进的A*算法的路径规划效果图。

A*算法算法改进前和改进后在32*32地图中搜索路径的信息对比如表3所示。

表3优化前后的A*算法对比

对于搜索速度的优化：仿真过程中打印当前节点的位置信息发现算法在搜索求解中拓展了过多的无用节点，拓展节点越多、搜索效率越低的结论，图12展示了32*32栅格尺寸下某一场景的拓展节点图。

从仿真实验中，选取了三组随机地图进行了比对实验，通过分析三组实验结果，可以得出的结论为：加入转向惩罚函数的优化A*算法相比传统A*算法规划出的路径折点大幅减少，且它们之间的最短路径长度相等；加入了转向惩罚函数的改进A*算法扩展出了更多的搜索节点。

本发明优化主要针对启发函数的优化，在仿真实验中，为启发函数设计了一个权重值以增加启发函数的影响力，如图13-图15分别展现使用不同权值的启发函数在路径规划中的不同表现，叉表示扩展的节点。

通过图13-图15的比对中发现简单环境下设置不同权重的扩展节点随着启发函数的比重增加而减少并且这里所需设置的启发函数需要很大的占比才能造成一个扩展节点的变化，通过图16-图18的比对中发现复杂环境下只对启发函数需设置很小的权重系数，拓展的搜索节点就有可能形成比较少的效果，另外当启发函数设置的权重过大时，搜索也出现了额外的拓展节点并且路径变差了的情况。通过对以上现象的总结以及多次仿真实验的试错。为了减少搜索时产生过多节点和搜索效率的低下的问题设计了启发函数的动态加权方法，前期采用了动态加权的搜索算法能够加快前期的搜索速度，后期采用的加权策略主要是为了找出一条更优的路径，而不会导致错过最佳的当前节点。

所述改进的A*算法中代价函数还表示为：

f(n)＝g(n)+w*h(n)；

其中，f(n)为节点n的移动代价，g(n)为节点n距离起点的代价，h(n)为节点n距离终点的预计代价，w为动态参数。动态参数变更的主要策略为距离目标点的距离，经过多次实验这里的距离最后使用直线距离d来作为动态参数w的触发器。w设置为1.2,和0.95。

d＝math.hypot(n1.x-n2.x,n1.y-n2.y)；

其中，math.hypot函数是Python中的math模块提供的一种输入直角三角形的两直角边长的两个值，然后返回边斜长的一个方法，作用等同于使用欧式距离公式，n1.x表示节点n1的x坐标值，n2.x表示节点n2的x坐标值，n1.y表示节点n1的y坐标值，n2.y表示节点n2的y坐标值。

若节点n与所述目标点的距离大于设置距离，则w＝1.5，否则w＝0.95。

将动态加权的方法应用在A*算法中随机生成障碍物环境中进行路径规划实验，与传统A*遍历的节点数与路径长度对比见表4。

表4改进A*算法在随机地图中的遍历节点数据

通过表5可以看出，改进后的算法在70*70栅格地图中，搜索时扩展的节点数显著减少的同时也兼顾了后期搜索的解的最优性，与最优解的路径距离基本等同，少数情况大于最优解的路径距离，综合所述改进算法的搜索效率相比传统A*算法有了显著的提升。

本发明主要针对传统A*算法在不同地图规模中规划出的路线中折点过多的缺点和在搜索过程中扩展了过多无用节点造成搜索效率低的缺点，分别设计了转向惩罚函数和动态加权的方法，通过分析仿真实验结果表明：改进后的A*算法在规划路径中的折点更少，搜索效率更高。

本说明书中各个实施例采用递进的方式描述，每个实施例重点说明的都是与其他实施例的不同之处，各个实施例之间相同相似部分互相参见即可。

本文中应用了具体个例对本发明的原理及实施方式进行了阐述，以上实施例的说明只是用于帮助理解本发明的方法及其核心思想；同时，对于本领域的一般技术人员，依据本发明的思想，在具体实施方式及应用范围上均会有改变之处。综上所述，本说明书内容不应理解为对本发明的限制。