一种基于KM算法的机器人-任务分配方法

技术领域

本发明属于机器人领域领域，具体涉及一种基于KM算法的机器人-任务分配方法。

背景技术

机器人领域中任务分配的应用包括搜救任务、巡逻行动等，如攻击或监视，物理灾害管理等。如何智能化地实现多机器人系统多任务分配是无人装备领域的热点话题。

在多机器人系统中用于解决任务分配问题的主要技术是基于拍卖(或市场)的方法，基于博弈论的方法，基于优化的方法(启发式算法，匈牙利算法等)和机器学习技术。根据所使用的技术，可以找到最优或几乎总是近似的解决方案，各种方法存在不同程度的可伸缩性、复杂性和适应性。基于拍卖的技术通常具有较高的计算成本，使得它们不适用于大规模系统。此外，确定性优化技术在大中型系统中具有较高的计算成本和较低的可扩展性，但它们适合于小型系统(比如系统中只有4台机器人)，在小型系统中具有非常好的效率。博弈论方法具有非常低的成本，使它们成为提供具有中等到良好效率的快速解决方案的理想选择，这些方法也可以用于大型系统，因为它们具有非常好的可伸缩性。启发式和学习方法成本适中，效率高，可扩展性好，根据具体问题，可以在中等规模的环境中使用，有时也可以在更大规模的环境中使用，机器学习技术在动态任务分配和动态环境中非常突出，但多数模型停留在学术实验室环境，目前很难在现实中落地。鉴于某些应用场景属于小型系统(机器人数量小于10)，基于确定性优化的方法(比如匈牙利算法)有较高的计算效率，且能寻找到问题的最优解，但在无法找到完备匹配的情况下，匈牙利算法将无法找到最优解。

本发明采用基于Kuh_Munkras(KM)算法的机器人-任务分配方法，相比于传统的枚举法和启发式算法，KM算法的精度和速度都具有明显优势，能够更好地适应机器人领域的实时性和准确性要求。

发明内容

(一)要解决的技术问题

本发明要解决的技术问题是如何提供一种基于KM算法的机器人-任务分配方法，以解决多机器人系统中的任务分配问题。

(二)技术方案

为了解决上述技术问题，本发明提出一种基于KM算法的机器人-任务分配方法，该方法包括如下步骤：

S1、首先初始化机器人集合和任务目标集合的节点顶标值，其中，v1为待分配的任务集合，v2为机器人集合；设v1中顶标为lx[i],v2中顶标为ly[j]，为满足

S2、然后，在二分图中找出所有节点和满足找出lx[i]+ly[j]＝W[i,j]的边构成的子图，即相等子图；

S3、在相等子图中使用匈牙利算法搜索最大匹配，并判断该最大匹配是否为完备匹配，若是，则输出该完备匹配，即为最佳匹配，结束流程；若否，修改可行顶标值，继续寻找相等子图，重复上述步骤。

(三)有益效果

本发明提出一种基于KM算法的机器人-任务分配方法，本发明与现有技术相比的优点在于：

本发明提供了一种易于实现、高效且有效的机器人任务分配方法，此算法在稠密图上的效率高于其他算法，可以应用于多机器人系统执行巡逻营救等分配任务中。

附图说明

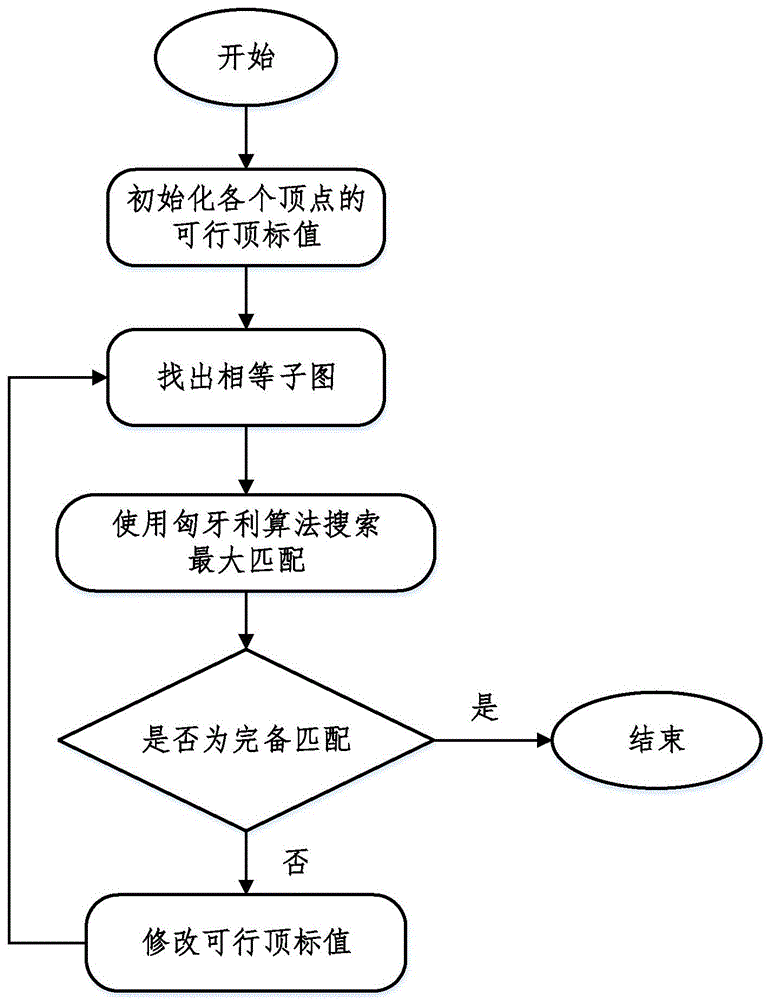
图1为本发明的任务分配KM算法执行流程示意图；

图2为KM算法的第一步；

图3为KM算法的第二步；

图4为KM算法的第三步；

图5为KM算法最终匹配结果。

具体实施方式

为使本发明的目的、内容和优点更加清楚，下面结合附图和实施例，对本发明的具体实施方式作进一步详细描述。

本发明涉及机器人-任务分配方法，特别是指一种基于Kuh_Munkras(KM)算法的机器人-任务分配方法。

本发明的目的在于提供一种高效且准确的机器人任务分配方法，使机器人系统可以根据自身载荷自主分配任务目标，保证完成所有任务的总耗时最小。

该发明提出了一种基于KM算法的机器人任务分配方法，将整数规划问题转化为二分图最佳匹配问题，通过匈牙利算法求解二分图最大匹配问题，进而使用KM算法求解最佳匹配问题。

机器人-任务分配问题可以描述为：n个机器人分配n项任务，一个机器人只能分配一项任务，一项任务只能分配给一个机器人，一个机器人做某项任务是需要特定时间的，如何分配任务，保证总时间开销最小。

记x

x

令C＝(c

机器人-任务分配问题可以进一步转化为二分图最佳匹配问题。

二分图是一种特殊的图结构，假设图G＝是一个二分图,其所有的顶点可以划分为满足下列条件的两个子集v1,v2：在E中任取一条边,

二分图的匹配问题在有限资源分配时经常会用到，其是为了保证某一个资源分且只分到某一个用户的手中。二分图匹配问题可以看成是二分图的一个子图g，该子图g满足以下条件：在这个子图g中，不存在有任意的两条边依附于同一个顶点。

在二分图的匹配当中，有两种常见的匹配目标，一个是最大匹配，即尽可能多地将v1,v2中的点配对；另一个是最佳匹配，最佳匹配的应用场景则是在带权二分图中，v1中所有的点都与v2中的某一个点匹配成对，并且能够使得这些边的权值之和最大。假设在任务分配中，权值表示机器人做某项任务时间的倒数，则可以通过求二分图的最佳匹配将每项任务分配给特定机器人，并且使得完成所有任务的总时间最短。

匈牙利算法是一种易于理解且易于使用的算法，可以解决二分图最大匹配问题，其核心思想在于寻找增广路。假定ei已经是分配好的边，ci是尚且没有分配的边，如果存在路径类似于c0～e0～c1～e1～...～cm,从尚未分配的边开始寻找，在途中分配、未分配交替出现，最后结尾与一条未分配的边，这样的路径称为增广路。

匈牙利算法的计算过程如下：

S11、初始化已经匹配好的边集合

S12、寻找增广路path，把路径上所有边的匹配状态取反，得到一个更大的匹配S'；

S13、重复第S12步，直至图中不存在增广路。

该算法依次尝试给每一个v1集合节点x寻找一个匹配的v2集合节点y，y能与x匹配，需要满足如下两个条件之一：

(2)y本身是非匹配点：此时无向边(x,y)本身就是非匹配点，自己构成一条长度为1的增广路。

(2)y已经与v1中其中一个点x’匹配，但从x’出发能找到另一个v2中的点y’与之匹配：此时路径x～y～x’～y’为一条增广路。

在程序实现时，采用深度优先搜索的框架，递归地从x出发寻找增广路；若找到，则在深搜回溯时，把路径的匹配状态取反。另外，可以用全局bool数组标记节点的访问情况，避免重复搜索。

上述匈牙利算法找到了最大匹配，接下来使用KM算法寻找最佳匹配。

在KM算法中，涉及到完备匹配的概念，完备匹配即v1中所有的点都与v2中的某一个点匹配成对，也就是一方的点已经完全匹配。

设M是一个带权二分图的完备匹配，给定每一个点一个顶标，不妨设v1中顶标为lx[i],v2中顶标为ly[j],如果对于任意的∈M,都有lx[i]+ly[j]＝W[i,j]，则M是一个最佳匹配。

KM算法在求解一个最佳匹配时，首先需要用匈牙利算法来进行匹配，如果能找到满足定理中所要求的lx[i]+ly[j]＝W[i,j]条件的完备匹配，那么就找到最佳匹配。但是在查找的过程中，可能无法找到这样的完备匹配，只能找到当前的最大匹配，此时若最大匹配不是最佳匹配，需要来更新顶标，从而使得找最佳匹配的过程继续下去。假设此时已经在v1遍历的点为p,在v2中遍历的点为q，取s∈p,t∈(v2-q),r∈q,计算增量d＝min(lx[s]+ly[t]-W[s,t]),然后更新顶标lx[s]-d，ly[r]+d,然后再用匈牙利算法来进行匹配。重复上述过程，最后找到最佳匹配。

实施例1：

本发明为一种基于Kuh_Munkras(KM)算法的机器人-任务分配方法。

图1为本发明的基于Kuh_Munkras(KM)算法的机器人-任务分配方法流程示意图。

S1、首先初始化机器人集合和任务目标集合的节点顶标值，其中，v1为待分配的任务集合，v2为机器人集合；设v1中顶标为lx[i],v2中顶标为ly[j]，为满足

S2、然后，在二分图中找出所有节点和满足找出lx[i]+ly[j]＝W[i,j]的边构成的子图，即相等子图。

S3、在相等子图中使用匈牙利算法搜索最大匹配，并判断该最大匹配是否为完备匹配，若是，则输出该完备匹配，即为最佳匹配，结束流程；若否，修改可行顶标值，继续寻找相等子图，重复上述步骤。

一种基于Kuh_Munkras(KM)算法的机器人-任务分配方法，步骤如下：

1)机器人任务分配问题的数学描述。

为n个机器人分配n项任务，一个机器人只能分配一项任务，一项任务只能分配给一个机器人，一个机器人做某项任务是需要特定时间的，如何分配任务，保证总时间开销最小。

记x

x

令C＝(c

2)将规划问题转化为二分图最佳匹配问题。

二分图是一种特殊的图结构，假设图G＝是一个二分图,其所有的顶点可以划分为满足下列条件的两个子集v1,v2：在E中任取一条边,

二分图的匹配问题在有限资源分配时经常会用到，其是为了保证某一个资源分且只分到某一个用户的手中。二分图的匹配可以看成是二分图的一个子图，该子图满足以下条件：在这个子图g中，不存在有任意的两条边依附于同一个顶点。

在二分图的匹配当中，有两种常见的匹配目标，一个是最大匹配，即尽可能多地将v1,v2中的点配对；另一个是最佳匹配，最佳匹配的应用场景则是在带权二分图中，v1中所有的点都与v2中的某一个点匹配成对，并且能够使得这些边的权值之和最大。假设在任务分配中，权值表示机器人做某项任务时间的倒数，则可以通过求二分图的最佳匹配将每项任务分配给特定机器人，并且使得完成所有任务的总时间最短。

3)使用匈牙利算法解决二分图最大匹配问题，其核心思想在于寻找增广路。

匈牙利算法的计算过程如下：

1.初始化已经匹配好的边集合

2.寻找增广路path，把路径上所有边的匹配状态取反，得到一个更大的匹配S'；

3.重复第2步，直至图中不存在增广路。

该算法依次尝试给每一个v1集合节点x寻找一个匹配的v2集合节点y，y能与x匹配，需要满足如下两个条件之一：

(1)y本身是非匹配点：此时无向边(x,y)本身就是非匹配点，自己构成一条长度为1的增广路。

(2)y已经与v1中其中一个点x’匹配，但从x’出发能找到另一个v2中的点y’与之匹配：此时路径x～y～x’～y’为一条增广路。

4)使用KM算法寻找最佳匹配。

在KM算法中，涉及到完备匹配的概念，完备匹配即v1中所有的点都与v2中的某一个点匹配成对，也就是一方的点已经完全匹配。

设M是一个带权二分图的完备匹配，给定每一个点一个顶标，不妨设v1中顶标为lx[i],v2中的为ly[j],如果所有的边∈M,都有lx[i]+ly[j]>＝W[i,j],W[i,j]是边的权值，如果对于任意的∈M,都有lx[i]+ly[j]＝W[i,j]，则M是一个最佳匹配。

KM算法在求解一个最佳匹配时，首先需要用匈牙利算法来进行匹配，如果能找到满足定理中所要求的lx[i]+ly[j]＝W[i,j]条件的完备匹配，那么就找到最佳匹配。但是在查找的过程中，可能无法找到这样的完备匹配，只能找到当前的最大匹配，此时需要来更新顶标，从而使得找最佳匹配的过程继续下去。假设此时已经在v1遍历的点为p,在v2中遍历的点为q，取s∈p,t∈(v2-q),r∈q,计算增量d＝min(lx[s]+ly[t]-W[s,t]),然后更新顶标lx[s]-d，ly[r]+d,然后再用匈牙利算法来进行匹配。重复上述过程，最后找到最佳匹配。

实施例2：

下面是一个简单例子说明KM算法的过程：

假设有4个机器人4项任务，各个机器人对各项任务完成的效率(即KM算法中的权重矩阵)如表1所示。

表1权重矩阵W

(1)探索第一步，为机器人x1分配任务：按照KM算法初始化顶标lx＝[3,4,6,7],ly＝[0,0,0,0],由于lx[1]+ly[2]＝W[1,2],所以为x1分配y2。如图2所示。

(2)探索第二步，为机器人x2分配任务：由于lx[2]+ly[2]＝W[2,2]，而任务y2已被分配，寻找增广路x2～y2～x1～y4(lx[1]+ly[4]＝W[1,4])，因此x1匹配y4,x2匹配y2。如图3所示。

(3)探索第三步，为机器人x3分配任务：由于lx[3]+ly[2]＝W[3,2]，而任务y2已被分配，寻找增广路x3～y2～x2～y3(lx[2]+ly[3]＝W[2,3])，因此x1匹配y4，x2匹配y3，x3匹配y2。如图4所示。

(4)探索第四步，为机器人x4分配任务：图中无增广路，本次匈牙利算法所能找到的最大匹配已经达到，但是最佳匹配还没有完成。根据KM算法更新顶标，首先求解d,此时在v1遍历的点为{x1,x2,x3,x4}，在v2中遍历的点为{y2,y3,y4},从而求得d＝min

lx＝[2,3,5,6],ly＝[0,1,1,1]。

(5)探索第五步，根据新顶标值重新找最佳匹配，发现仍然无法为机器人x4分配任务，因此需要继续更新顶标值...

最终当顶标值为lx＝[-4,-3,-1,0],ly＝[0,7,7,7]时，由于lx[1]+ly[4]＝W[1,4],lx[2]+ly[3]＝W[2,3],lx[3]+ly[2]＝W[3,2],lx[4]+ly[1]＝W[4,1],因此可以找到图5所示的最佳匹配，即：x1匹配y4,x2匹配y3,x3匹配y2,x4匹配y1。如图5所示。

本发明与现有技术相比的优点在于：

本发明提供了一种易于实现、高效且有效的机器人任务分配方法，此算法在稠密图上的效率高于其他算法，可以应用于多机器人系统执行巡逻营救等分配任务中。

以上所述仅是本发明的优选实施方式，应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明技术原理的前提下，还可以做出若干改进和变形，这些改进和变形也应视为本发明的保护范围。