一种解决量子电磁问题的方法及系统

技术领域

本发明涉及电磁研究领域，特别是涉及一种基于空间滤波的高阶时域有限差分解决量子电磁问题的方法及系统。

背景技术

计算电磁学(Computational Electromagnetics，CEM)在当今各种电子设备中电磁效应(辐射、散射或传播)的建模和仿真中占据重要地位。其应用包括但不限于通信、生物成像和诊断、电磁兼容性或干扰、信号完整性分析等。近年来，现代电子技术的迅速发展使得集成电路相关的元器件特征尺寸缩减到纳米级别，单位体积内物质存储和信息处理的能力达到百万倍的提升，极大的促进了计算机等智能化小型化电子设备的迅速发展。然而，由于其纳米尺度结构的空间尺寸与电子的德布罗意波长相比拟，因此量子效应已经不可忽略，关于表面等离激元的量子特性也在实验中不断被发现。因此，基于经典电磁理论的建模方案已经无法满足纳米电子设备的设计和仿真需求，微观量子系统-宏观电磁系统的多物理场建模、仿真，已成为高频、高速、宽带和多功能集成电磁元器件与芯片小型化发展过程中迫切需要解决的科学问题，也是纳米电子与信息技术需要攻克的核心技术难题。

由于电子被困在亚波长范围内，电子态将被量子化，因此电子的运动应遵循薛定谔方程。同时，激发的电子产生量子电流，辐射电磁场。因此，为了精确地描述电磁场与微观粒子之间的相互作用机理，需要将麦克斯韦方程与薛定谔方程(Maxwell-

同样重要的是，针对M-S耦合方程的数值求解也是多物理问题研究的重点。由于麦克斯韦方程和薛定谔方程都是关于时域和空域的微分方程，针对此类耦合方程，在时间和空间上具有二阶精度的时域有限差分(FDTD(2,2))方法及其改进方法被证明是最有效和最简洁的方法之一。例如，FDTD(2,2)方法已成功用于求解M-S方法，模拟人工原子(量子点)与电磁场的相互作用过程。然而传统FDTD(2,2)方法的显式差分策略，其时间步长受计算空间中网格尺寸的限制，需要满足CFL稳定性条件。对于纳米电磁系统，网格尺寸处于纳米/亚纳米级别，较小的时间步长将急剧降低仿真效率。为此，将显式FDTD(2,2)方法和隐式无条件稳定FDTD方法相结合来求解M-S耦合方程。由于隐式FDTD方法的无条件稳定特性，可采用较大的时间步长来提高计算效率。然而，对于A-φ方程来说，采用隐式的FDTD方对其进行数值求解并不容易，这是因为A-φ方程在时间域和空间域具有二阶偏导数，使得基于FDTD方法的数值实现较为困难。此外，传统FDTD(2,2)方法在时间和空间上只有二阶精度，数值色散误差较大，在长时间的数值模拟中会产生较大的误差累计，甚至导致数值结果发散。针对FDTD(2,2)数值误差较大的缺点，一些学者提出了采用高阶FDTD方法用于模拟电磁系统，高阶FDTD方法在具备普通FDTD(2,2)方法简单和容易实现的同时，数值色散误差得到改善。然而，HO-FDTD方法是显式算法，仍然需要满足CFL稳定性条件。

发明内容

本发明的目的是提供一种基于空间滤波的高阶时域有限差分解决量子电磁问题的方法及系统，不仅能够满足CFL稳定性条件，还能够缩小计算时间，提高计算效率。

为实现上述目的，本发明提供了如下方案：

一种基于空间滤波的高阶时域有限差分解决量子电磁问题的方法包括：

将量子电磁耦合系统中的电磁部分通过求解达朗贝尔方程和外加电磁作用下的薛定谔方程的自洽耦合方程组得到FDTD方法的矢量磁位、标量电位、波函数和量子电流的迭代公式；

根据各所述迭代公式，确定外加电磁作用下的CFL稳定性条件和滤波半径；

对所述滤波半径进行空间滤波操作，得到满足CFL稳定性条件的滤波半径；

根据所述满足CFL稳定性条件的滤波半径对量子电磁耦合系统进行数值色散计算分析，得到数值色散误差。

可选地，所述将量子电磁耦合系统中的电磁部分通过求解达朗贝尔方程和外加电磁作用下的薛定谔方程的自洽耦合方程组得到FDTD方法的矢量磁位、标量电位、波函数和量子电流的迭代公式，具体包括：

在均匀媒质空间情况下，确定量子电磁耦合系统中的矢量磁位的迭代公式：

确定量子电磁耦合系统中的标量电位的迭代公式：

其中，J为电流源项，

对于量子部分，在外加电磁作用下，确定粒子的波函数迭代公式：

其中，ψ是量子机制中描述粒子在位置r和时间t处量子态的概率振幅的波函数；m

确定粒子运动产生的量子电流的迭代公式：

可选地，所述电磁作用下的CFL稳定性条件为：

其中，Δt为时间步长，Q

所述滤波半径为：

其中，R为滤波半径，k

可选地，所述对所述滤波半径进行空间滤波操作，得到满足CFL稳定性条件的滤波半径，具体包括：

根据所述滤波半径在每一次的数值迭代过程中加入空间滤波操作，滤除因采用不满足CFL稳定性条件的大时间步长而产生的空间高频分量，得到满足CFL稳定性条件的滤波半径。

一种基于空间滤波的高阶时域有限差分解决量子电磁问题的系统包括：

量子电磁耦合系统迭代公式确定模块，用于将量子电磁耦合系统中的电磁部分通过求解达朗贝尔方程和外加电磁作用下的薛定谔方程的自洽耦合方程组得到FDTD方法的矢量磁位、标量电位、波函数和量子电流的迭代公式；

稳定性条件和滤波半径确定模块，用于根据各所述迭代公式，确定外加电磁作用下的CFL稳定性条件和滤波半径；

满足CFL稳定性条件的滤波半径确定模块，用于对所述滤波半径进行空间滤波操作，得到满足CFL稳定性条件的滤波半径；

数值色散误差确定模块，用于根据所述满足CFL稳定性条件的滤波半径对量子电磁耦合系统进行数值色散计算分析，得到数值色散误差。

可选地，所述量子电磁耦合系统迭代公式确定模块，具体包括：

矢量磁位的迭代公式确定单元，用于在均匀媒质空间情况下，确定量子电磁耦合系统中的矢量磁位的迭代公式：

标量电位的迭代公式确定单元，用于确定量子电磁耦合系统中的标量电位的迭代公式：

其中，J为电流源项，

波函数迭代公式确定单元，用于在外加电磁作用下，确定粒子的波函数迭代公式：

其中，ψ是量子机制中描述粒子在位置r和时间t处量子态的概率振幅的波函数；m

量子电流的迭代公式，用于确定粒子运动产生的量子电流的迭代公式：

可选地，所述电磁作用下的CFL稳定性条件为：

其中，Δt为时间步长，Q

所述滤波半径为：

其中，R为滤波半径，k

可选地，所述满足CFL稳定性条件的滤波半径确定模块，具体包括：

空间滤波操作单元，用于根据所述滤波半径在每一次的数值迭代过程中加入空间滤波操作，滤除因采用不满足CFL稳定性条件的大时间步长而产生的空间高频分量，得到满足CFL稳定性条件的滤波半径。

根据本发明提供的具体实施例，本发明公开了以下技术效果：

本发明提供一种基于空间滤波的高阶时域有限差分解决量子电磁问题的方法，将量子电磁耦合系统中的电磁部分通过求解达朗贝尔方程和外加电磁作用下的薛定谔方程的自洽耦合方程组得到FDTD方法的矢量磁位、标量电位、波函数和量子电流的迭代公式；根据各迭代公式，确定外加电磁作用下的CFL稳定性条件和滤波半径；对滤波半径进行空间滤波操作，得到满足CFL稳定性条件的滤波半径；根据满足CFL稳定性条件的滤波半径对量子电磁耦合系统进行数值色散计算分析，得到数值色散误差。本发明不仅能够满足CFL稳定性条件，还能够缩小计算时间，提高计算效率。

附图说明

为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。

图1为本发明基于空间滤波的高阶时域有限差分解决量子电磁问题的方法流程图；

图2为k

图3为q阶空间差下CE随k

图4为不同CE

图5为B＝0.2,CE＝3时，SF-HO-FDTD(2,q)方法的数值色散误差；

图6为B＝0.2时，SF-HO-FDTD(2,4)(q＝4)方法的数值色散误差随CE的变化曲线；

图7为B＝0.3,CE＝3时，q阶空间差分下的数值色散误差；

图8为B＝0.05时，四阶空间差分下数值色散误差随CE的变化曲线；

图9为不同时间步下观察点矢量磁位对比图；

图10为不同时间步下薛定谔方程的本征态；

图11为纳米管的几何模型；

图12为基态和第一激发态的本征波函数示意图；

图13为不同时间步下纳米管中电子概率分布；

图14为不同时间步下基态与第一激发态转换图；

图15为纳米管中的电子第二激发态与第三激发态概率波包；

图16为不同时间步下纳米管中电子概率分布；

图17为不同时间步下多态量子态占比随时间的变化；

图18为本发明基于空间滤波的高阶时域有限差分解决量子电磁问题的系统结构图。

具体实施方式

下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

本发明的目的是提供一种基于空间滤波的高阶时域有限差分解决量子电磁问题的方法及系统，不仅能够满足CFL稳定性条件，还能够缩小计算时间，提高计算效率。

为使本发明的上述目的、特征和优点能够更加明显易懂，下面结合附图和具体实施方式对本发明作进一步详细的说明。

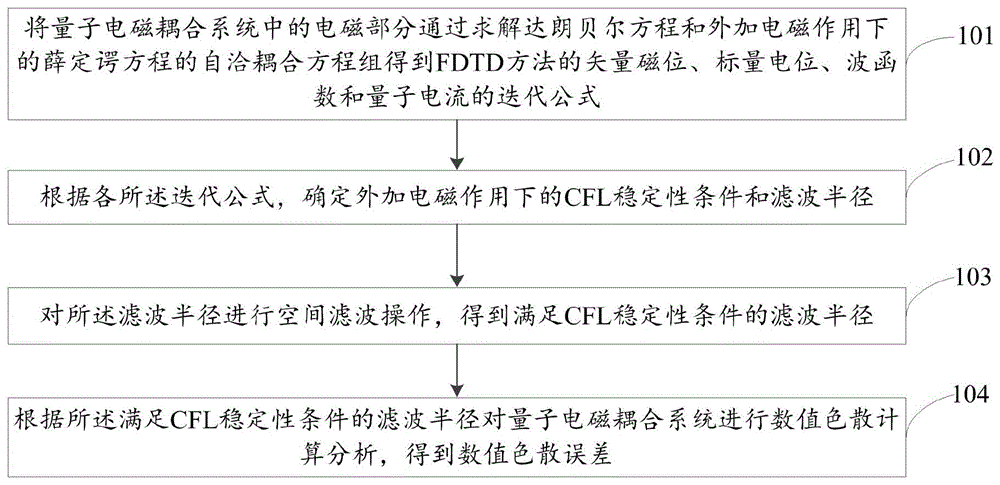
图1为本发明基于空间滤波的高阶时域有限差分解决量子电磁问题的方法流程图。如图1所示，一种基于空间滤波的高阶时域有限差分解决量子电磁问题的方法包括：

步骤101：将量子电磁耦合系统中的电磁部分通过求解达朗贝尔方程和外加电磁作用下的薛定谔方程的自洽耦合方程组得到FDTD方法的矢量磁位、标量电位、波函数和量子电流的迭代公式，具体包括：

在均匀媒质空间情况下，确定量子电磁耦合系统中的矢量磁位的迭代公式：

标量电位(φ)的时间演化过程可由如下方程表述：

其中，J表示电流源项，公式(1)为达朗贝尔方程，公式(2)为简单的洛伦兹规范。

对于量子部分，在外加电磁作用下，修正的薛定谔方程可写成如下形式：

其中，ψ是粒子的波函数；m

公式(1)-(4)可构建一个自洽的量子-电磁多物理耦合系统，模拟光与物质的相互作用过程。

步骤102：根据各所述迭代公式，确定外加电磁作用下的CFL稳定性条件和滤波半径。

在公式(1)和(2)中，位函数(A-φ)在时间上的偏导数采用二阶差分近似，其离散形式可写成如下形式：

其中，n表示采样时刻。

不失一般性，在不考虑电流源的情况下，公式(5)可采用如下矩阵形式进行表示：

P

其中

P＝(A

其中

三维平面波定义为：

其中,Φ表示各个场分量的幅度，ζ是增长因子，k

令

对公式(5)中位函数进行如公式(11)-(14)所示的空间离散，并对其空间一阶和二阶偏导数进行q阶差分近似得(以A

其中C

表1一阶导数的q阶并置差分系数

表2二阶导数的q阶并置差分系数

采用同样差分近似方法，其他电磁分量(A

接着，将公式(7)-(14)，(16)-(17)和其他场方向的电磁分量离散公式带入公式(6)并简化得：

[ζ

其中：

为了得到公式(18)的非零解，其系数矩阵M的行列式的值必须为0，通过对公式(19)化简得到：

根据公式(22)，得到增长因子ζ的值为

为了保证数值算法的稳定性，增长因子ζ的模值必须小于等于1。显然，ζ

将公式(21)代入公式(24)得:

取

可以得到关于时间步长Δt的不等式：

其中，Δx＝Δy＝Δz＝Δ。公式(27)即为采用HO-FDTD(2,q)方法数值求解位函数方程(公式(1)和公式(2))的时间稳定性条件。

对于外加电磁场作用下的修正薛定谔方程，公式(3)可化简成如下形式：

公式(27)可写成一个特征值问题，即

这里λ是特征值：

对公式(29)的时间偏导进行二阶差分近似得：

为了保证系统的稳定性，增长因子

|g|＝|ψ

将公式(32)带入公式(31)得：

为了使得|g|≤1，必须有

考虑波函数是平面波的情况，即

与电磁部分处理方法相同，对波函数的一阶和二阶空间偏导数进行q阶差分近似得(以x方向为例)：

波函数在其他方向的处理方式相同。

根据公式(36)和(37)，方程(30)中λ可推导成如下形式：

同时，根据不等式(34)

其中

公式(39)即为采用HO-FDTD(2,q)方法数值求解修正的薛定谔方程(公式(3))的时间稳定性条件。可以看出，时间步长的取值不仅与网格尺寸有关系，还与场分量A，φ和势阱V有关系。如果不考虑外加电磁场的影响(A＝0和φ＝0)，同时根据公式(26)

公式(42)为无外加电磁作用下，采用HO-FDTD(2,q)方法数值求解薛定谔方程的时间稳定性条件。

对于电磁系统，通过公式(27)可知，利用HO-FDTD(2,q)方法求解位函数方程需要满足时间稳定性条件。然而，若在公式(25)中，假定波函数被限制在一个以k

同时假定Δx＝Δy＝Δz＝Δ，将公式(43)代入公式(25)得：

其中，d＝k

令

则关于时间步长的不等式可写成如下形式：

随θ，/>

其中，Δt

对于量子系统，采用上述类似的方法，HO-FDTD(2,q)方法数值求解薛定谔方程的时间稳定性条件(公式(42))可被扩展为：

对于公式(48)和(50)，当CE的值确定后，可以得到k

步骤103：对所述滤波半径进行空间滤波操作，得到满足CFL稳定性条件的滤波半径，具体包括：

根据所述滤波半径在每一次的数值迭代过程中加入空间滤波操作，滤除因采用不满足CFL稳定性条件的大时间步长而产生的空间高频分量，得到满足CFL稳定性条件的滤波半径。

以电磁系统为例，当CE

步骤104：根据所述满足CFL稳定性条件的滤波半径对量子电磁耦合系统进行数值色散计算分析，得到数值色散误差。

以下分别通过量子系统和电磁系统进行数值色散分析：

量子系统：

不失一般性，在不考虑外加电磁场的影响下(A＝0和φ＝0)，采用高阶FDTD(2,q)方法求解方程(3)的色散关系式可以写成如下形式：

式中，

在公式(52)中，将Δt

薛定谔方程的解析色散关系式为：

定义数值色散误差Err

定义Δ＝B/k

图5为CE＝3时,SF-HO-FDTD(2,q)方法求解薛定谔方程的数值色散误差。可以看出，当SF-HO-FDTD(2,q)(q＝4,6,8)方法的时间步长是传统HO-FDTD(2,q)方法的最大时间步长的3倍时(Δt

图6给出了SF-HO-FDTD(2,4)(q＝4)方法在不同时间步长情况下的数值色散误差(CE＝1,5,7,10)。可以发现，随着CE的增大，数值误差变大，这与实际情况相符。但值得注意的是，即使CE＝10，SF-HO-FDTD(2,4)方法仍具有较低的数值色散误差。

电磁系统：

在公式(22)中，令增长因子ζ＝e

其中，

图7为CE＝3时,SF-HO-FDTD(2,q)方法求解位函数方程的数值色散误差。可以看出，当SF-HO-FDTD(2,q)(q＝4,6,8)方法的时间步长是传统HO-FDTD(2,q)方法的最大时间步长的3倍时(Δt

图8给出了SF-HO-FDTD(2,4)(q＝4)方法在不同时间步长情况下的数值色散误差(CE＝1,5,7,10)。可以发现，随着CE的增大，数值误差变大，这与实际情况相符。但值得注意的是，即使CE＝10，SF-HO-FDTD(2,4)方法仍具有较低的数值色散误差。

通过对SF-HO-FDTD(2,q)方法的数值色散分析可以发现，SF-HO-FDTD(2,q)方法具有较低的数值色散误差。同时，与传统HO-FDTD(2,q)方法的数值特性类似，采用更高阶的数值差分近似方法会降低数值色散误差。然而，在实际应用中，较高阶的数值近似方法往往会降低数值计算效率，这是因为它具有更高的数值复杂度。因此在一般的数值仿真中，需要在保证计算精度的同时兼顾数值计算效率。。

实施例1：偶极子源

为了验证本发明所提SF-HO-FDTD(2,q)方法的正确性和有效应，首先利用SF-HO-FDTD(2,q)方法求解位函数方程(公式(1)和公式(2))，模拟电偶极子源在三维空间的电磁辐射问题。不失一般性，本发明所有例子中选择q＝4。电偶极子处于仿真空间的中心，仿真区域包含70×70×70个网格，网格尺寸大小Δx＝Δy＝Δz＝5cm，计算空间采用Mur吸收边界条件进行截断。探测点距离辐射源50cm，辐射源采用高斯脉冲，其形式为

分别采用传统HO-FDTD(2,4)方法(CE＝1)和SF-HO-FDTD(2,4)方法(CE＝5,10)数值求解了位函数方程，得到探测点处A

实施例2：3D量子阱

第二个例子为三维量子阱模型，研究其本征频率和本征态问题。三维量子阱模型的尺寸为L

表3HO-FDTD(2,4)与SF-HO-FDTD(2,4)计算三维量子阱的特征频率结果比较

实施例3：量子-电磁多物理场耦合模型

量子-电磁多物理场耦合模型如图11所示，被限制在纳米管中的电子在外加电磁场的作用下，其电子波包的量子态会发生转变，同时电子波包会发生运动，运动产生的量子电流与电磁激励源相叠加重新作用于电磁系统，电磁系统和量子系统之间的相互作用过程，形成一个自洽的多物理耦合系统。在图11所示的准一维模型中，电磁空间的尺寸为120Δx×120Δy×120Δz，采用Mur吸收边界条件对计算空间进行截断。纳米管的空间尺寸为Δx×Δy×100Δz，其在z方向所加的势阱表达式为：

其中，V

在此势阱下，通过求解非时变薛定谔方程，可以得到基态和第一激发态的本征波函数，如图12所示。

在多物理场仿真中，为了确保数值结果的稳定性，整个仿真系统采用统一的时间步长，该时间不长需要同时满足电磁系统和量子系统的CFL条件。根据仿真参数和电磁系统的CFL稳定性条件)，电磁系统的最大离散时间步长Δt

图13为纳米管中电子波包的波形随时间的变化过程，其中图12(a)为传统HO-FDTD(2,4)方法计算所得结果，图13(b)，(c)，(d)所示为采用不同时间步长的SF-HO-FDTD(2,4)方法，。从图13(a)可以发现电子波包在初始时刻以单峰形式存在(对应基态)，在2-8s时间段内快速振荡，最后在10s后以双峰的形式呈现(对应第一激发态)。同时为了定量描述电子量子态的转换率，转换率因子定义如下

其中，y

图14所示为采用不同时间步长的SF-HO-FDTD(2,4)方法和传统HO-FDTD(2,4)方法计算所得电子量子态的转换率，可以发现，采用传统HO-FDTD(2,4)方法和SF-HO-FDTD(2,4)方法数值求解多物理场耦合方程，都可以实现电子量子态的完美越跃迁。此外，从图13和图14可以发现，SF-HO-FDTD(2,4)方法与传统HO-FDTD(2,4)方法计算结果吻合较好，这也验证了本发明所提SF-HO-FDTD(2,4)方法求解多物理方程的正确性。

此外，利用SF-HO-FDTD(2,4)方法数值求解多物理耦合系统模拟了电子量子态的多态转换过程。图15为电子第二激发态和第三激发态的概率波包。图16和图17分别为纳米管中电子波包的波形随时间的变化过程和电子量子态的转换率。从图16和图17可以发现，采用SF-HO-FDTD(2,4)方法求解多物理耦合方程可以实现电子量子态的完美跃迁，且与传统HO-FDTD(2,4)方法计算结果一致，验证了本发明所以SF-HO-FDTD(2,4)方法的正确性。

同时，针对以上多物理场耦合方程的数值求解，给出了HO-FDTD(2,4)方法和SF-HO-FDTD(2,4)方法数值计算效率。从表4可以看到，当CE

表4FDTD(2,4)和SF-FDTD(2,4)方法计算量子态的多态转换的执行时间

相较于经典理论，基于半经典理论的量子-电磁多物理耦合模型需要联合求解更多的数学方程，因此数值实现困难。虽然传统的FDTD(2,2)方法及其改进方法能够实现有效求解这些多物理耦合方程组，但传统的FDTD(2,2)方法数值误差较大，在长时间的数值迭代中容易产生较大的误差累计。而且，传统的FDTD(2,2)方法是显式算法，其时间步长受计算空间中网格尺寸的限制，计算效率差。在空间上具有高计算精度的HO-FDTD(2,q)方法能够有效降低的FDTD(2,2)方法的数值色散误差，但其仍是显式算法，需满足时间稳定性条件的限制，因此计算效率有待进一步的提高。相较于显式方法，隐式的FDTD方法具有无条件稳定的特性，即时间步长不受网格尺寸的限制，在数值仿真中采用较大的时间步长能够提高计算效率。但隐式的FDTD方法往往需要对多物理方程进行特殊的时间和空间离散化处理，导出的迭代公式往往较为复杂，数值实现相较于显式方法更加困难。本发明所提出的SF-HO-FDTD(2,q)方法，在保留了传统HO-FDTD(2,q)方法空间上的高精度特性的同时，又可突破其时间稳定性条件的限制。另外，SF-HO-FDTD(2,q)方法不需要修改传统HO-FDTD(2,q)方法的数值迭代公式，只需在每一次的数值迭代中加入滤波操作即可，因此数值实现较为容易。总的来说，本发明的创新点主要包含以下两点:1)推导了基于HO-FDTD(2,q)方法处理位函数方程和修正的薛定谔方程的CFL稳定性条件；2)将SF方法应用于HO-FDTD(2,q)，提出了SF-HO-FDTD(2,q)方法并将其应用于求解多物理耦合方程。论文中提出的三个数值算例，包含电偶极子辐射问题，量子阱本征态问题和电子量子态调控的多物理场耦合问题都有效的证明了本发明所提方法的正确性和有效性。

图18为本发明基于空间滤波的高阶时域有限差分解决量子电磁问题的系统结构图。如图18所示，一种基于空间滤波的高阶时域有限差分解决量子电磁问题的系统包括：

量子电磁耦合系统迭代公式确定模块201，用于将量子电磁耦合系统中的电磁部分通过求解达朗贝尔方程和外加电磁作用下的薛定谔方程的自洽耦合方程组得到FDTD方法的矢量磁位、标量电位、波函数和量子电流的迭代公式；

稳定性条件和滤波半径确定模块202，用于根据各所述迭代公式，确定外加电磁作用下的CFL稳定性条件和滤波半径；

满足CFL稳定性条件的滤波半径确定模块203，用于对所述滤波半径进行空间滤波操作，得到满足CFL稳定性条件的滤波半径；

数值色散误差确定模块204，用于根据所述满足CFL稳定性条件的滤波半径对量子电磁耦合系统进行数值色散计算分析，得到数值色散误差。

所述量子电磁耦合系统迭代公式确定模块201，具体包括：

矢量磁位的迭代公式确定单元，用于在均匀媒质空间情况下，确定量子电磁耦合系统中的矢量磁位的迭代公式：

标量电位的迭代公式确定单元，用于确定量子电磁耦合系统中的标量电位的迭代公式：

其中，J为电流源项，

波函数迭代公式确定单元，用于在外加电磁作用下，确定粒子的波函数迭代公式：

其中，ψ是量子机制中描述粒子在位置r和时间t处量子态的概率振幅的波函数；m

量子电流的迭代公式，用于确定粒子运动产生的量子电流的迭代公式：

所述电磁作用下的CFL稳定性条件为：

其中，Δt为时间步长，Q

所述滤波半径为：

其中，R为滤波半径，k

所述满足CFL稳定性条件的滤波半径确定模块203，具体包括：

空间滤波操作单元，用于根据所述滤波半径在每一次的数值迭代过程中加入空间滤波操作，滤除因采用不满足CFL稳定性条件的大时间步长而产生的空间高频分量，得到满足CFL稳定性条件的滤波半径。

本说明书中各个实施例采用递进的方式描述，每个实施例重点说明的都是与其他实施例的不同之处，各个实施例之间相同相似部分互相参见即可。对于实施例公开的系统而言，由于其与实施例公开的方法相对应，所以描述的比较简单，相关之处参见方法部分说明即可。

本发明中应用了具体个例对本发明的原理及实施方式进行了阐述，以上实施例的说明只是用于帮助理解本发明的方法及其核心思想；同时，对于本领域的一般技术人员，依据本发明的思想，在具体实施方式及应用范围上均会有改变之处。综上所述，本说明书内容不应理解为对本发明的限制。