一种基于L2,1范数的大规模数据快速聚类方法

技术领域

本发明涉及机器学习、数据分析领域，具体涉及基于L

背景技术

聚类分析也称集群分析，是数据统计与数据分析领域的重要组成部分，也是无监督学习任务中被研究最多、应用也最为广泛的一种技术。聚类分析根据数据中样本的特征，将数据划分为多个不同大小的簇，使研究人员可以初步了解数据空间的结构和特点，同时也为下一步的数据分析、数据处理等环节奠定了基础。

随着互联网、大数据和人工智能等技术应用于社会生活的各个领域，其产生的海量数据需要通过聚类分析来处理。然而，传统的聚类方法在处理这些大规模数据时已经很难满足人们对计算速度和精确度的要求。同时，真实数据中存在着大量非线性和非高斯分布的噪声，这些噪声难以去除，极大地影响了聚类结果的准确性。

发明内容

本发明的目的是进一步提高聚类分析技术在面对大规模数据集聚类任务时的性能，使聚类过程在拥有快速计算特性的同时，消除大规模数据中的噪声影响，达到较高的精确度。

为了达到上述目的，本发明采用如下技术方案：

一种基于L

步骤1：粗聚类结果生成：采用K-means方法对原始数据操作生成粗聚类结果；

设X＝{x

这样做有三个好处：

一是初始聚类可以给出数据的粗略聚类结果，以便于可以在方法的第二步中直接基于矩阵C定义一个优化问题(聚类细化)；

二是方法的最终结果是初始聚类和聚类细化两个步骤相结合的。由于这两个步骤都倾向于从不同的方面(基于划分聚类和图谱聚类)学习簇结构，因此方法在检测簇结构方面更容易获得数据的真实完整结构；

三是由于不同的数据在不同的聚类方法下表现不一，所以可以根据情况选择恰当的适合第一步的基本聚类方法。

步骤2：生成锚点及锚点图：采用K-means方法生成锚点，并基于高斯核函数进行度量生成锚点图。

为了进一步对需要求解的矩阵进行降维，本方法先在原始数据上采用K-means方法生成m(c＜m＜n)个锚点，然后利用锚点图的拉普拉斯矩阵作为正则约束完成谱聚类细化的步骤。由此，就可将第二步中参与计算的矩阵大小从(n×d)降维至(n×m)。通过选择大小恰当的m，方法可以在保留原始数据中的重要结构的基础上，大大降低方法的时间和空间复杂度。选用K-means方法生成锚点而非随机生成锚点的原因在于，大量实践证明，对于相同数量的锚点，使用K-means方法生成的锚点往往能在后续的聚类过程中取得更优的性能。

设U＝{u

式中，G

本方法使用高斯核函数ψ定义x

其中，参数σ是一个可以通过经验确定的自由参数。a，b均为任意维度相等的向量。

步骤3：基于锚点图的拉普拉斯矩阵进行谱聚类。

考虑到谱聚类具有如下优点：

(1)谱聚类只需要数据之间的相似度矩阵，因此对于处理稀疏数据的聚类很有效。这点传统聚类方法比如K-means很难做到。

(2)由于方法中使用了降维操作，因此在处理高维数据聚类时的时间和空间复杂度比传统聚类方法好。

(3)谱聚类能够识别出数据中的各种簇结构。在方法的第二步，对初始结果进行基于谱聚类的细化。

由此，得到数据集X与其锚点图G之间对应的相似度矩阵W：

W＝GG

设

步骤4：使用L

由上述步骤，本方法的目标函数表述如下：

Q(Y)＝||C-Y||

其中，||C-Y||

上式中，目标函数Q(Y)的第一项为重构误差，可以保证最终的聚类结果尽可能地获取到K-means方法和谱聚类方法结果的相同结构。而Q(Y)的第二项与著名的拉普拉斯正则化方法密切相关，用于基于图的学习。上述用于聚类细化的L

首先，将聚类问题转化为L

其次，由于初始聚类的第一步,可以直接定义指示矩阵C上的目标函数，从而在C上对离群点和异常值进行处理。

最后，通过引入拉普拉斯算子的正则化，可以利用谱聚类方法揭示大规模聚类的聚类结构。更值得注意的是，这一方法可以很容易地将解Y限制在由拉普拉斯矩阵的主要特征向量张成的空间内，从而减少方法的计算时间。

步骤5：迭代优化，得到聚类结果。

为保证在应用于大规模数据聚类时，兼具可靠的计算效率；使用非负矩阵分解将目标函数中的最大概率聚类矩阵Y转换为V

其中，

令

通过引入两个辅助变量E＝C-V

其中，μ、Λ

求解目标函数最小值的具体求解流程如下：

更新辅助变量Z：

目标函数在固定E和H

等价于：

Z的解可由上式获得：

更新辅助矩阵H

目标函数在固定辅助变量E和Z的情况下可以转换为如下形式：

其中，Tr(·)表示括号中矩阵的转置。

同样地，可以得到：

辅助矩阵H

更新辅助变量E：

目标函数在固定辅助矩阵H

令X＝C-V

因此，辅助变量E的解为：

更新辅助矩阵Λ

Λ

Λ

更新参数μ：

μ＝ρμ

其中，1＜ρ＜2。

通过更新以上参数，得到目标函数Q(Y)取得最小值时，V

本方法使用WebKB和Cora两个常用的真实数据集测试了本方法和其他针对大规模数据的典型方法的聚类性能。

其中，WebKB是一种广泛应用于聚类方法的真实文本数据集，本发明采用其中WebKBCornell、WebKBTexas、WebKBWashington和WebKBWisconsin共计4017个样本点，共4组数据的数据集来测试所有方法的性能。

Cora数据集作为计算机科学领域的研究论文集，包含2708个科学出版物，分为7个类别。类似地，这里采用包含1617个样本的CoraML数据集作为本方法的测试数据。

为了验证本方法对比主流针对大规模数据的聚类方法的优势，选取了几种典型的针对大规模数据的快速聚类方法LSSC、NMF、FNMTF、LPFNMTF和FRWL作为对比方法。对比方法的详细情况总结如下：

(1)LSSC(Large Scale Sparse Clustering)

一种大规模稀疏聚类方法。使用L

(2)NMF(Nonnegative Matrix Factorization)

使用非负矩阵分解的大规模数据聚类方法。对于任意给定的矩阵M，NMF方法可以求解到两个非负矩阵W和H，从而将矩阵M表示为W和H的乘积，而后两个矩阵的维度要小于初始矩阵。由此NMF方法能够将高维数据矩阵降维，很适合用于处理大规模数据。

(3)FNMTF(Fast Nonnegative Matrix Tri-factorization)

一种基于非负矩阵分解的大规模数据快速聚类方法。它将因子矩阵直接约束为聚类指示矩阵(一种特殊的非负矩阵)。通过新的约束，将方法原本的优化问题分解为许多小的多的子问题，使该方法特别适用于处理真实世界的大规模数据。并提出了一种只包含少量矩阵乘法的优化方法。

(4)LPFNMTF(Locality Preserve FNMTF)

一种新的局部保留正则化的FNMTF方法。该方法通过增加流形正则化来实现对两个分解因子矩阵的几何约束。

(5)FRWL(Fast Spectral Clustering based on Random-Walk Laplacian)

一种基于随机游走拉普拉斯矩阵(Random-Walk Laplacian，RWL)的谱聚类方法。显式地平衡了锚点的比重和数据点的独立性，对边界数据的聚类效果得到了提升。

(6)FCLSD(Fast Clustering for Large-scale Data)

即本发明中提出的方法。

本发明的有益效果如下：

本发明在对大规模数据聚类的过程中，对计算机硬件性能要求低，聚类准确度高。通过引入L

附图说明

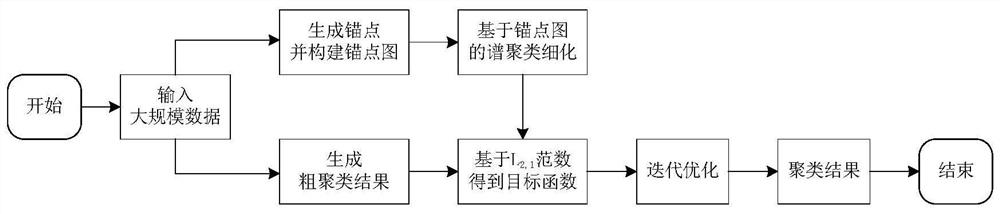
图1为本发明方法的总体流程图。

图2(a)为不同锚点数在WebTexas数据集上对应的聚类结果；图2(b)为不同锚点数在WebTexas数据集上对应的计算时间；图2(c)为不同锚点数在WebWisconsin数据集上对应的聚类结果；图2(d)为不同锚点数在WebWisconsin数据集上对应的计算时间。

图3(a)为不同λ在WebTexas数据集上对应的聚类结果；图3(b)为不同λ在WebTexas数据集上对应的计算时间；图3(c)为不同λ在WebWisconsin数据集上对应的聚类结果；图3(d)为不同λ在WebWisconsin数据集上对应的计算时间。

图4(a)和图4(b)分别为为本方法在两个不同数据集上的收敛性分析。

具体实施方式

下面结合附图对本发明做进一步说明。

本发明的具体实施的流程图如图1所示，包含步骤如下：

步骤1：粗聚类结果生成；

步骤2：生成锚点及锚点图；

步骤3：基于锚点图的拉普拉斯矩阵进行谱聚类；

步骤4：得到目标函数；

步骤5：迭代优化，得到聚类结果。

步骤1的具体实现步骤为：

给定数据集X，使用K-means方法对原始数据进行操作，将其分为c类，得到一个大小为n×c的粗聚类指示矩阵C，其每一行中只有一个元素为1，其余元素均为0。

步骤2的具体实现步骤为：

人为的选取锚点数m，并采用K-means方法选取锚点的位置，并构建锚点图。

设U＝{u

式中，G

本方法使用高斯核函数定义x

其中，参数σ是一个可以通过经验确定的自由参数。a，b均为任意维度相等的向量。

步骤3的具体实现步骤为：

在得到锚点图之后，我们使用锚点图对应的拉普拉斯矩阵，得到目标函数的图约束项，进行谱聚类。具体如下：

由步骤1和步骤2，得到数据集X与其锚点图G之间对应的相似度矩阵W：

W＝GG

设

步骤4的具体实现步骤为：

使用L

目标函数表述如下：

Q(Y)＝||C-Y||

其中，||C-Y||

步骤5的具体实现步骤为：

使用非负矩阵分解将目标函数中的最大概率聚类矩阵Y转换为V

其中，

令

通过引入两个辅助变量E＝C-V

其中，μ、Λ

求解目标函数最小值的具体求解流程如下：

更新辅助变量Z：

目标函数在固定E和H

等价于：

Z的解由上式获得：

更新辅助矩阵H

目标函数在固定辅助变量E和Z的情况下转换为如下形式：

其中，Tr(·)表示括号中矩阵的转置；

同样地，得到：

辅助矩阵H

更新辅助变量E：

目标函数在固定辅助矩阵H

令X＝C-V

因此，辅助变量E的解为：

更新辅助矩阵Λ

Λ

Λ

更新参数μ：

μ＝ρμ

其中，1＜ρ＜2；

通过更新以上参数，得到目标函数Q(Y)取得最小值时，V

本方法包括其他对比方法在不同数据集上的聚类准确度和聚类纯度，如表1所示，运行时间如表2所示。

从表1中展示的结果可以看出，本方法在大部分数据集上的聚类准确度和聚类纯度都优于参与对比实验的其他聚类方法。LSSC、NMF、FNMTF、LPFNMTF、FRWL和本方法在5个实验数据集上平均聚类准确度分别为：0.3939、0.1767、0.3691、0.1747、

表1

表2

在几种方法的计算时间上，LSSC、NMF、FNMTF、LPFNMTF、FRWL和本方法在5个实验数据集上平均计算时间分别为：0.4124、15.5323、19.0256、18.6744和0.6706秒。可以看出本方法的计算时间在略微弱于LSSC的情况下，计算时间只有其他算法的1/25。这充分说明了本方法在面对大规模数据时，计算的高效性。

结合表1与表2中展示的结果可以看出，本方法使用与LSSC方法相当、甚至比其他对比方法低出数10倍的计算时间，取得了在大部分数据集上更佳的聚类准确度和聚类纯度，这充分说明了本方法性能的优越性。

影响本方法性能和效率的主要有两个参数，分别是锚点个数和正则项系数。图2(a)、图2(b)、图2(c)和图2(d)分别给出了在采用不同锚点数时，本方法在WebTexas数据集和WebWisconsin数据集上运行的实验结果。从图中可以看出，当锚点数量较少时，本方法的聚类准确度表现一般。但是随着锚点数量的增加，聚类准确度与锚点数量呈现出正相关。接着当锚点数量增加到一定程度时，聚类准确度相对稳定，不再增长。因此，选择合适的锚点数量对于聚类结果的准确度有着至关重要的影响。同时，随着锚点数量的不断增加，计算时间虽有略微增长，但算法的时间代价始终保持在一个较低的水平。

图3(a)、图3(b)、图3(c)和图3(d)分别展示了当采用不同大小的正则项系数时，本方法在WebTexas数据集和WebWisconsin数据集上运行的实验结果，包括在聚类准确度、聚类纯度和计算时间上的差异。从图中不难看出，总体上当正则项系数变大时，聚类纯度相对稳定，而聚类准确度则有着明显的提升。但当正则项系数的值超过一定的阈值后，聚类准确度保持不变，甚至反而出现了下降。因此，选择合适正则项系数值对于聚类结果的准确度有很大的影响。另一方面，本方法的计算时间随着正则项系数的增加，总体保持稳定的波动。

结合图2(a)、图2(b)、图2(c)和图2(d)以及图3(a)、图3(b)、图3(c)和图3(d)中展示的信息来看，锚点数量和正则项系数的大小均对实验结果有着不同程度的影响。其中，聚类准确度受二者的影响较大，聚类纯度受影响较小。同时，锚点数量对算法的计算时间有着较大的影响，而正则项系数则对计算时间的影响较弱。

本方法在WebWisconsin和CoraML数据集上的目标函数值和算法求解时迭代次数的关系图，如图4(a)和图4(b)所示。从图4(a)和图4(b)中可以看出，本方法在WebWisconsin数据集上进行迭代约100次后，目标函数值达到收敛，在CoraML数据集上进行迭代约70次后达到收敛。这可以说明，在不同的数据集上，本方法的收敛速度是不同的。但综合而言，较少的迭代次数都说明了本方法在大规模数据上计算的有效性以及可靠性。