基于自由振动信号的贝叶斯模态识别及不确定性分析方法

技术领域

本发明涉及模态识别技术领域，特别是涉及一种基于自由振动信号的贝叶斯模态识别及其不确定性分析方法。

背景技术

在结构健康监测、模态参数识别、结构模型修正、结构损伤诊断等识别技术领域中，Brincke提出了一种用于轻阻尼结构模态参数估计的频域分解方法。该方法使用功率谱密度计算模态参数，采用奇异值分解估计模态，并使用峰值拾取法确定自振频率。随后，将每个单自由度系统转换到时域，使用对数衰减法则计算结构阻尼比。尽管该方法具有抗噪性和对密集频率模态有一定分辨率的优点，但其阻尼比识别效果不佳，仅适用于小阻尼、近似白噪声激励的结构。增强的频域分解法在计算阻尼比方面具有更大的优势，但在计算相关函数时对数据进行截断可能会导致识别结果与理论值不同。Cole等人最初提出了随机减量法，它通常用于计算汽车、飞机等结构的自由响应，并已在航天飞机的模型结构实验中得到应用。该方法假设外部激励是平稳白噪声，其期望值为零。根据该理论，结构的响应信号由两个信号组成，即确定部分和随机部分。其中，确定部分由结构自身性质、初始条件等决定，而随机部分则由外部激励引起。Yang等提出了一种改进的非线性特征系统识别算法，使用实验数据对该方法进行了评估，结果证明，所提出的方法在准确识别模态参数和验证结果方面是有效的。

对于模态识别，基于贝叶斯理论的模态识别方法的优势在于，不仅可以将模态参数识别出来，还可评估识别结果的不确定性。由于考虑了识别过程中的不确定性，该方法为结构模态分析提供了更加合理的分析措施，不确定性的量化值为健康监测、模型更新等领域提供了重要的决策依据。关于贝叶斯FFT方法的研究较少，依然存在着可以深入研究的问题：贝叶斯FFT方法在实际工程中的应用大多数为环境激励形式，而在自由振动等情形的实际应用研究较少，对自由振动等形式下的贝叶斯方法和实际工程应用需进一步研究实现。

发明内容

本发明针对上述问题，提供了一种基于自由振动信号的贝叶斯模态识别及其不确定性分析方法，本发明的技术方案如下：

一种基于自由振动信号的贝叶斯模态识别方法，所述方法包括以下步骤：

步骤1、根据数据计算的频谱，从中选择自振频率{f

步骤2、根据公式

表示n个测量自由度的第i阶模态振型向量；m是要识别模态的数量，

ω

步骤3、根据公式

表示(Φ

b

步骤4、对公式

μ

E(·|θ')表示给定θ'情况的条件期望；

步骤5、根据公式

本发明的另一技术方案为：一种对上述获取的模态参数进行不确定性分析方法，包括以下步骤：

S1、根据模态参数

S2、对S1计算得到的Hessian矩阵H

S3、根据公式

S4、后验协方差矩阵C的对角元素即为模态参数最可能值的方差，任一模态参数z

本发明提供了一种基于自由振动信号的贝叶斯模态识别及其不确定性分析方法，基于贝叶斯傅里叶变换原理，引入了有限时间傅里叶变换，基于待识别的模态参数，将模态参数集进一步分解并利用负对数似然函数求解得到待识别的模态参数的最可能值；在得到模态参数的最可能值基础上，计算负对数似然函数关于模态参数的导数得到特征值和特征向量，并以此得到后验协方差矩阵，最终确定模态参数最可能值的方差，以及任一模态参数最可能值的变异系数，本发明提供的方法可对自由振动等形式下进行贝叶斯模态识别以及实际工程应用。

附图说明

图1是本发明实施例中基于自由振动信号的贝叶斯模态识别方法流程示意图；

图2是本发明实施例中对获取的模态参数进行不确定性分析方法流程示意图。

具体实施方式

下面结合附图和实施例对本发明作进一步的详细说明。可以理解的是，此处所描述的具体实施例仅仅用于解释本发明，而非对本发明的限定。另外还需要说明的是，为了便于描述，附图中仅出示了与本发明相关的部分而非全部结构。

在更加详细地讨论示例性实施例之前应当提到的是，一些示例性实施例被描述成作为流程图描绘的处理或方法。虽然流程图将各步骤描述成顺序的处理，但是其中的许多步骤可以被并行地、并发地或者同时实施。此外，各步骤的顺序可以被重新安排。当其操作完成时所述处理可以被终止，但是还可以具有未包括在附图中的附加步骤。所述处理可以对应于方法、函数、规程、子例程、子程序等等。

本发明实施例针对一种基于自由振动信号的贝叶斯模态识别及其不确定性分析方法，提供了如下实施例：

基于本发明的实施例1

本实施例用于说明模态参数识别方法，具体包括：

1参数识别原理

1.1引入FTFT

假设一个n个自由度的理想力学结构，初始时刻用人工方法给予激励，然后让它产生自由振动。在忽略环境激励的情况下，自由振动阶段的加速度测量响应

式中

ε

N——采样点的总数量；

n——测量自由度的数量。

误差项ε

式中i——-1的均方根；

Δt——采样时间间隔。

设θ表示待识别的模态参数集合，其包括三组需要识别的参数。第一组为{f

贝叶斯框架下，似然函数表达式为：

C

式中det(·)——行列式计算；

μ

C

I

μ

式中

满足式(6)：

式中ζ

ω

第i阶模态位移η

式中η

——自由振动响应的第i阶模态速度；

T——数据持续时长；

ω

对式(6)两边取FTFT，得到：

将式(7)、(8)、(9)代入式(10)，得到：

Q

对式(12)重新合并整理，得到：

重新整理式(13)，得到：

式(14)中，h

式中β

将式(14)代入式(9)，得到：

式(17)中，各变量的定义如下：

式中u

v

1.2目标函数重构

将式(5)重新写成如下的矩阵形式：

式中Φ——模态振型矩阵，

——模态加速度向量，/>

对式(22)取FTFT，得到了μ

式(23)中，各变量的定义如下：

基于上述内容，在改进方法中，待识别的模态参数θ中的第二组参数集可以定义成如上所述的{u

为求解模态参数的最可能值(MPV)，应使得式(3)中的似然函数最大。为便于分析计算，将该后验概率密度分布函数(PDF)p(θ|{F

p(θ|{F

则，NLLF化为：

上式为负对数似然函数(NLLF)。由于后验PDF在最可能值(MPV)处有一个唯一的最大值。等价地，NLLF在MPV处有一个唯一的最小值。对NLLF在MPV处展开二阶泰勒近似，得到后验PDF的高斯近似，即：

式中

n

后验MPV表征了模态参数的可能值，和协方差矩阵表征了在有限测量数据集下的不确定性。贝叶斯识别问题的目标即是计算出MPV和不确定性。

将式(4)代入式(29)，NLLF可以简化为：

观察上式NLLF的数学结构，可以将模态参数集θ分为S

关于S

由上式可知，在其他模态参数的MPV已知的情况下，可以计算出S

1.3线性分解振型

通常，J(θ′)，即NLLF对f

为了摆脱Φ(i)单位范数的约束，即||Φ(i)||＝1，令

Φ＝Φ

式(35)中，

因此，Φ

以Φ

式(39)中，

b

为了便于推导出{u

μ

式(41)中，各变量的定义如下：

将式(41)代入式(33)，得到w的二次形式：

式(44)中，

关于w对式(44)的二次型求最小值，得到{u

为了进一步推导出模态振型的MPV解析式，将式(39)改写为另一种形式：

式(48)中，

b

b

将式(48)代入式(33)，得到(Φ

式(51)中，

关于(Φ

通过观察，可以发现，Q

在模态振型

可以对上式进一步最小化，在数值优化过程中，{u

最后，Φ和{u

/>

基于本发明的实施例2

本实施例用于说明后验不确定性量化方法，具体包括：

2不确定性的定量解析

2.1计算原理

要定量评估结果的后验不确定性，则需要计算Hessian矩阵H

||Φ(i)||

由于在计算MPV时考虑了这些约束，则在推导NLLF的Hessian矩阵时也要正确反映该约束。故以归一化的形式显式写入振型，令

无论任何Φ(i)，都有

{λ

由于λ

接下来，本研究将推导NLLF的Hessian矩阵各项二阶偏导数的解析式。NLLF由式(63)给出(以归一化振型的形式)，即：

式(63)中，

式(64)中，

由式(66)给出：

由式(67)给出：

b

b

其中h

2.2建立二阶导函数解析式

下面将推导NLLF关于{f

θ′的组成如式(70)：

误差S

在z的MPV处，J

式中H

后验协方差矩阵C是块对角矩阵，由式(73)给出：

因此，可以分别确定θ′的后验协方差矩阵和S

式中

接下来需要计算J关于θ′的Hessian矩阵，即H

{f

式(75)中，“·”表示两个矩阵的元素与元素对应相乘得到新矩阵，∑[·]表示对应矩阵中所有元素的总和。

B

式(64)中J(θ′)的右侧第三项可以写为：

将式(75)和式(77)代入式(64)，得到：

令z

J(θ′)的二阶导数由式(80)给出：

式中δ

式(80)中的B

式中e

E

E

diag(·)表示由对应向量形成的对角矩阵。

2.3建立

基于式(79)，J关于z

J对Φ的分量的二阶导数是：

在上述几个式子中，涉及到很多

式中

的表达式如下：

式中

振型矩阵关于不同模态的振型分量的交叉导数为零，其表达式如下：

对同一阶模态s

2.4建立b

根据式(69)，b

b

和/>

b

/>

b

b

的表达式类似于/>

b

的表达式类似于/>

b

令z

2.5建立h

根据式(18)和(19)，h

h

/>

h

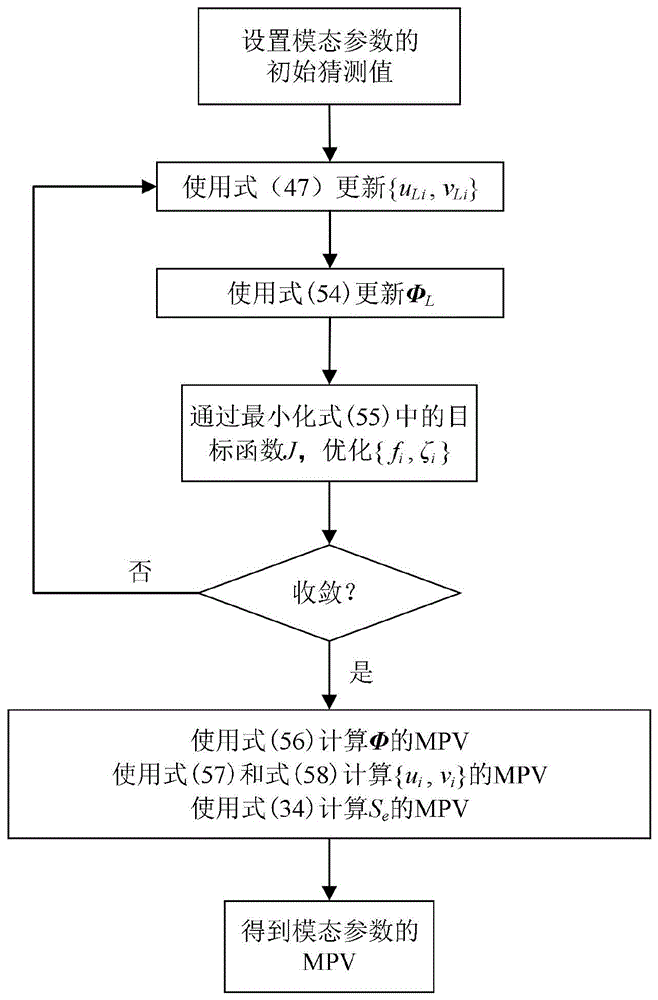
具体示例如图1所示，改进方法的MPV识别算法如下所述：

(1)使用matlab函数pwelch()计算数据的频谱，从中选择自振频率{f

(2)根据式(47)更新{u

(3)根据式(54)更新Φ

(4)数值最小化式(55)中的J，直到收敛，确定{f

(5)根据式(56)确定Φ的MPV；分别从式(57)和式(58)计算得到{u

具体示例如图2所示，后验协方差矩阵算法步骤如下所述：

(1)在模态参数

(2)对步骤(1)计算得到的Hessian矩阵H

(3)根据式(61)，忽略奇异性方向的特征值和特征向量，由式(62)计算得到后验协方差矩阵C，即H

(4)后验协方差矩阵C的对角元素即为模态参数MPV的方差，则任一模态参数z

式中，

本发明提供了一种基于自由振动信号的贝叶斯模态识别及其不确定性分析方法，基于贝叶斯傅里叶变换原理，引入了有限时间傅里叶变换，基于待识别的模态参数，将模态参数集进一步分解并利用负对数似然函数求解得到待识别的模态参数的最可能值；在得到模态参数的最可能值基础上，计算负对数似然函数关于模态参数的导数得到特征值和特征向量，并以此得到后验协方差矩阵，最终确定模态参数最可能值的方差，以及任一模态参数最可能值的变异系数，本发明提供的方法可对自由振动等形式下进行贝叶斯模态识别以及实际工程应用。

注意，上述仅为本发明的较佳实施例及所运用技术原理。本领域技术人员会理解，本发明不限于这里所述的特定实施例，对本领域技术人员来说能够进行各种明显的变化、重新调整和替代而不会脱离本发明的保护范围。因此，虽然通过以上实施例对本发明进行了较为详细的说明，但是本发明不仅仅限于以上实施例，在不脱离本发明构思的情况下，还可以包括更多其他等效实施例，而本发明的范围由所附的权利要求范围决定。