一种有向非平衡图上的局部全约束优化问题的分布式离散时间算法

技术领域

本发明涉及多智能体系统的分布式优化技术领域，特别涉及一种有向非平衡图上的局部全约束优化问题的分布式离散时间算法。

背景技术

随着大规模网络的兴起，分布式计算由于能够将一个复杂的计算任务分解成若干个子任务来减轻计算负担而受到越来越多的关注，这使得完成复杂计算任务的过程更加高效。分布式优化作为分布式计算的重要组成部分，由于其在多个领域的广泛应用，近年来也得到了广泛的研究。许多实际问题都可以归结为分布式优化问题，如机器学习问题、源定位问题、传感器网络中的估计问题、拥塞控制问题等。

关于分布式优化的研究主要分为无约束优化问题和约束优化问题。在实践中，相关的优化问题往往涉及到某种形式的约束。因此，从这个意义上说，研究分布式约束优化问题更有意义。在常见的方法中，一般采用连续时间算法来求解具有局部约束的分布式约束优化问题，然而，这些方法很难适用于网络拓扑非平衡有向的情况，因此，引入离散时间算法来对分布式优化问题进行求解。

现有的一些算法已经能够处理具有全局闭凸集约束的分布式优化问题，具有全局不等式约束的分布式优化问题，以及具有一般全局约束的分布式优化问题。此外，对于具有局部约束的分布优化问题，现有的一些算法已经解决了具有局部闭凸集约束和局部等式约束的优化问题以及具有局部等式约束和局部不等式约束的非凸分布优化问题等，但是这些结果不能直接应用于加权非平衡有向图的情形，所考虑的问题也没有涉及到一般的局部约束。因此，本发明的目的是设计一个新的离散时间算法，以解决加权非平衡有向图下具有一般局部约束的分布式优化问题。

发明内容

本发明主要考虑线性等式约束和凸不等式约束的在分布式优化中的处理方法，从而在有向非平衡图上设计分布式离散时间算法解决带有局部一般约束(包括线性等式约束、凸不等式约束和闭凸集约束)的凸优化问题，并给出严格的收敛性和收敛速率分析。

为了实现上述目的，本发明将通过如下的技术方案来实现：一种有向非平衡图上的局部全约束优化问题的分布式离散时间算法，包括以下步骤：

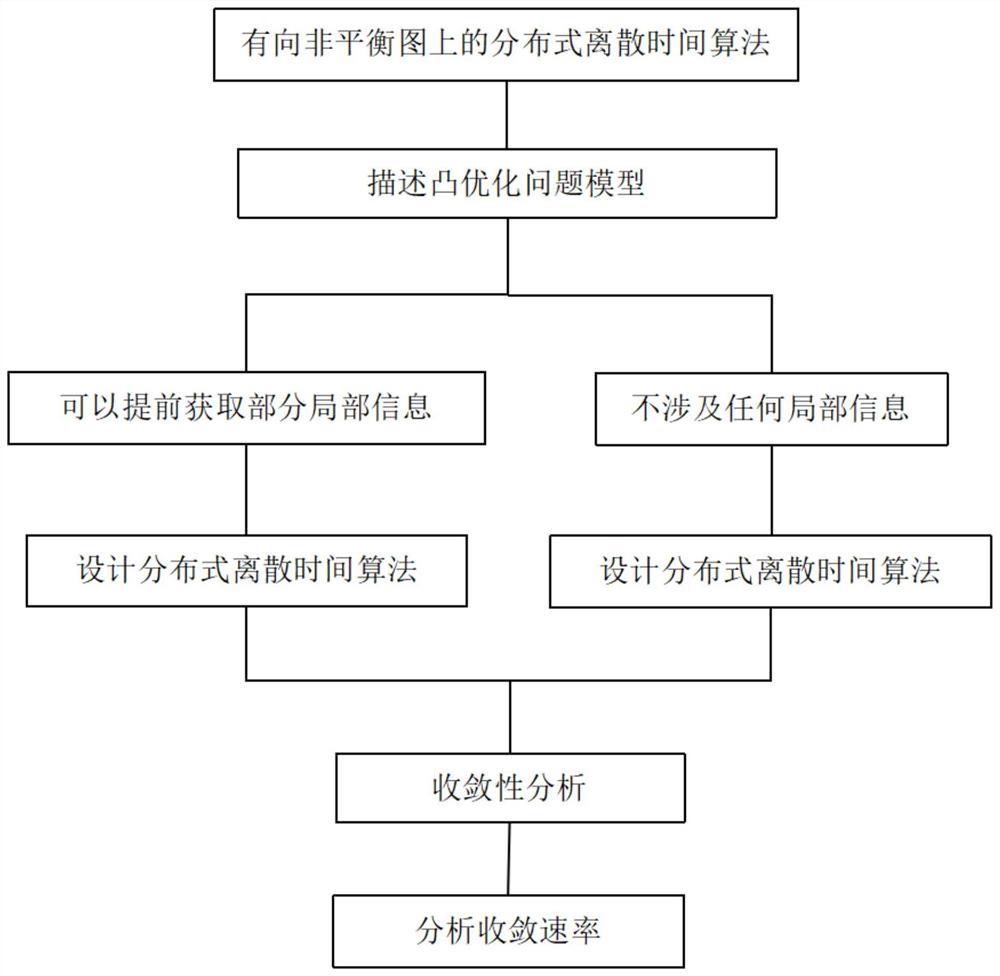
步骤1：对凸优化问题模型给出具体描述；

步骤2：在可以提前获取部分全局信息的情况下，在有向非平衡图上设计分布式离散时间算法；

步骤3：在不涉及任何全局信息的情况下，在有向非平衡图上设计分布式离散时间算法；

步骤4：对有向非平衡图上的分布式离散时间算法进行收敛性分析；

步骤5：分析分布式离散时间算法的收敛速率。

具体如下：

1.凸优化问题描述：

本发明主要考虑带有N个等式约束、N个不等式约束和N个闭凸集约束的凸优化问题，可以归结为

其中，

首先，关于上述的凸优化问题给出几个常见的假设。

假设1.1.存在一个向量

假设1.2.对于所有的i＝1，2，...，N，函数f

假设1.3.对于所有的i＝1，2，...，N，闭凸集X

假设1.4.存在一个正常数R使得对于任意的

注1.1.可以看出，若假设1.1成立，则最优解集X*非空。此外，假设1.2和假设1.3的引入主要是保证变量

2.分布式算法构建：

在这一节将考虑在固定有向非平衡图上针对两种不同的情况分别设计出分布式离散时间优化算法来解决凸优化问题(1)。

2.1第一种情形

在这一小节，假设每个节点都可以提前得到一些全局信息，包括向量

定义凸优化问题(2)相关的拉格朗日函数

其中g(x)＝(g

引理2.1.令假设1.1成立，且对于任意给定的向量

其中

易知对于任意的最优乘子μ

其中k′

此外，假设1.4在这一小节需要重新表述为如下的假设2.1。

假设2.1.存在一个正常数R使得对于任意的

基于以上的分析，在这一小节，有向非平衡图上的分布式离散时间算法设计为

其中，c

2.2第二种情形

在这一小节，考虑在无法提前得到任何全局信息的情况下，在有向非平衡图上设计完全分布式的离散时间算法来解决凸优化问题(1)，算法设计为

u

其中，

同时，β

下面将对两个算法做一些必要的说明。

注2.1.在给定的初始值条件下，通过迭代公式(6d)和(7e)更新的变量z

注2.2.容易看出，当在算法(7)中忽略处理不等式约束的项β(t)q

3.收敛分析准备工作：

在这一节，将为后面的收敛分析作一些准备工作，主要包括确立一些变量的上下界以及处理等式约束的一个重要引理。

注3.1.对于所有的i＝1，2，...，N，令

由于g

注3.2.若假设1.3成立，则从迭代公式(7d)可知对于所有的

这就意味着c

接下来，将给出一个处理等式约束的重要引理。

引理3.1.令

其中β″是一个满足条件0＜β″＜2的正常数，则对于Ω里满足条件Cs

证明：当Cu-b≠0时，记

显然d″为函数||Cx-b||在u处的梯度且||Cx-b||是关于x的凸函数，从而由(11)进一步可得

其中最后一个不等式的成立用到了性质Cs

因此，把(13)代入(12)可以得到(10)，从而得证。

4.收敛分析关键引理：

在这一节，将根据上一节的准备工作，来得到一些重要引理，为严格证明算法(7)的收敛性作准备。具体地，为了得到证明所需要的条件，在下述引理中验证在算法(7)下，对所有的t≥0和s

引理4.1.令假设1.1，假设1.2，假设1.3和假设1.4成立，则对于算法(7)和任意的s

其中

证明：从算法(7)可得

又由引理3.1可进一步得到

对于不等式(16)右侧的第一项，

其中

可以得到

其中第二个不等式的推导用到了函数

其中τ

其中τ

此外，由0＜β(t)≤β(0)≤1＜2可得0＜β(t)(2-β(t))＜2。令τ

由不等式(14)的形式可知，需要进一步分析

其中

进一步把不等式

和

代入(27)可得

从而有

其中

把不等式(29)代入(14)，同时在下面引理中对(14)做进一步处理。

引理4.2.令假设1.1，假设1.2，假设1.3和假设1.4成立，则对于算法(7)和任意的向量s

其中

证明：首先，令假设1.4成立，则

对于不等式(33)右侧的第二项，由

可进一步得到

同时，可以类似地得到

因此，把(35)和(34)代入(33)可得

其中τ

且对于所有的i＝1，2，...，N，η

其中，由于对于所有的t≥0，都有2-β(t)≥1，因此可以如在(32c)中定义的那样。此外，容易求得

η

从而由(38)和(39)可知

对于i＝1，2，...，N，由a

以及

最终，把(41)和(42)带入(40)可得(30)成立，从而得证。

5.收敛性主要定理：

在本节将基于前面两节的准备工作给出关于算法(7)的收敛性质的主要定理并给出严格的证明。

定理5.1.令假设1.1，假设1.2，假设1.3和假设1.4成立，则对于所有的i＝1，2，...，N，由算法(7)迭代的状态变量x

证明：令x

由α

可加。进一步由条件

另一方面，由于

进而由(49)可知

也就意味着

从(33)可得

接下来需要验证存在一个s

由于{s(t

另一方面，由(36)可知

因此有

其中

把上面不等式的两边都取下极限，由(50)和(51)可知

此外由

6.收敛速率主要定理：

在这一节将基于前三节的结果对所设计的分布式离散时间算法的收敛速率作具体的分析。

首先，定义变量

在接下来的定理中将具体地刻画算法(7)下的误差项和的上界，从而来描述算法的具体收敛速率。

定理6.1.令假设1.1，假设1.2，假设1.3和假设1.4成立，对于算法(7)，不等式

成立，其中

且

H

更进一步地，对于所有的i＝1，2，...，N，不等式

成立。

在给出定理6.1的具体证明之前，首先对定理6.1中给出的结果做一些必要的解释。

注6.1.把步长α(t)和β(t)所有需要满足的条件考虑在内，可以选取

从而由(57)可得

证明：[定理6.1的证明]由引理4.2可得

其中{a(k)}，{b(k)}，{c(k)}和{d(k)}与定理5.1中的定义相同，从而

其中

又因为

从而可得

因此由(59)可得

另一方面，由(36)可得

因此，结合(29)可得

又因为

所以

对于i＝1，2，由η

从而可得

其中

结合(67)，(68)和(69)可以得到

从而由(64)和(70)可得

此外，易得

选择

进一步地由函数f(x)和范数的凸性可得

把不等式(73)的两边同时除以

从而得证。

从算法(7)的收敛性分析和收敛速率分析，可以直接给出下面的推论来描述算法的(6)的收敛性和收敛速率，推论的证明可由定理5.1和定理6.1的证明直接给出，在此忽略。

推论6.1.令假设1.1，假设1.2，假设1.3和假设2.1成立，则对于所有的i＝1，2，...，N，在算法(6)迭代下的变量x

其中

注6.2.定理6.1描述了选择的步长与算法的收敛速率之间的关系，同时也可以直观地看出步长α(t)和β(t)所要求的的可加性条件的必要性。

相对于现有技术，该发明的优点如下：本发明主要研究了带有一般局部约束的凸优化问题，同时在可以提前获取部分全局信息和不涉及任何全局信息两种情况下分别在非平衡图上给出了分布式离散时间算法，同时严格给出了算法的收敛性分析并详细分析了算法的收敛速率。本发明工作最大的优点就是，在有向非平衡图上的分布式离散时间框架下，给出了有效处理等式约束和不等式约束的方法，避免了相应的乘子系统的引入，从而使收敛性易于分析。

附图说明

图1为算法结构示意图；

图2为带有二十个节点的强连通有向非平衡图；

图3为通过算法(7)更新的向量x

图4为通过算法(6)更新的向量x

图5为通过相关现有算法更新的向量x

具体实施方式

接下来根据附图并结合具体数值仿真实施方式来对本发明的技术方案作进一步阐述，并验证所设计算法的有效性。

考虑广泛存在于机器学习问题中的凸优化问题，其中目标函数为定义在

其中b

同时需要解决等式约束x

在matlab中的具体实施方式为：

首先给出图3的对应代码

该段代码可以实现图3的绘制，对于算法(7)，选择步长

接下来给出图4的对应代码

该段代码可以实现图4的绘制，对于算法(6)，选择惩罚因子k′

接下来给出图5的对应代码

该段代码可以实现图5的绘制，在只考虑闭凸集约束且其他的问题设定都相同的情况下，给出了相关现有算法在迭代下的状态变量的演化轨迹。

需要说明的是上述实施例，并非用来限定本发明的保护范围，在上述技术方案的基础上所作出的等同变换或替代均落入本发明权利要求所保护的范围。