一种电液伺服液压缸位置反馈控制系统

技术领域

本发明属于液压缸技术领域，具体地，涉及一种电液伺服液压缸位置反馈控制系统。

背景技术

液压缸是一种将液压能转变为机械能的装置，起作用是输出往复直线运动的力和速度，以驱动工作机构对外做功。

单出杆液压缸相对于双出杆液压缸具有工作空间小、结构简单等优点，在液压系统中应用十分广泛，尤其适用于空间有限、控制性能要求较高的使用场合。但是由于单出杆液压缸系统存在着严重的非线性问题和建模不确定性以及诸多弊端。如在对称阀控制单出杆非对液压缸电液伺服系统实现运动换向时，液压缸两腔容易出现气蚀和超压等现象，同时液压缸两腔面积不等导致正反向运动时液压系统刚度不等，造成系统动态特性不对称，特别是速度特性非对称，如果系统需要达到正反向运动最大速度相等，则增加了系统对流量的需求，从而增加了液压源的体积和成本。因此，为单出杆液压缸系统设计高性能的控制器异常困难。

发明内容

发明目的：本发明的目的是提供一种电液伺服液压缸位置反馈控制系统，解决了在传统控制方式越来越难以满足单出杆液压缸系统高精度控制要求的情况下，亟需一种简单实用且满足系统高精度控制性能需求的控制方法的问题。

技术方案：本发明提供了一种电液伺服液压缸位置反馈控制系统，包括控制器、伺服放大器、伺服阀、液压缸和传感器，所述控制器的信号输出端与伺服放大器连接，所述伺服放大器与伺服阀连接，所述伺服阀与液压缸的两腔体连接，并且伺服阀控制液压缸两腔体内液体的流动，所述液压缸通过传感器将位置信息反馈至控制器的信号输入端。

进一步的，上述的电液伺服液压缸位置反馈控制系统，建立液压缸两腔体的流量连续方程为：

其中，

上面公式中各个量代表的含义为：

——液压缸无杆腔、有杆腔的压力；

——活塞位移；

——活塞运动速度；

——体积弹性模量；

——液压缸无杆腔、有杆腔的活塞面积；

——液压缸无杆腔、有杆腔的体积；

——液压缸无杆腔、有杆腔的初始容积；

——液压缸无杆腔、有杆腔的流量；

——阀芯位移；

——阀流量系数；

——伺服阀面积梯度；

——油液密度；

——供油压力和回油压力。

进一步的，上述的电液伺服液压缸位置反馈控制系统，在液压缸两腔体的流量连续方程中，忽略液压缸两腔体的体积变化，则

进一步的，上述的电液伺服液压缸位置反馈控制系统，根据流量-输入信号的特性曲线得到下面的公式：

其中，

上面公式中：

——伺服阀的流量-信号增益；

——面积比；

——控制输入信号；

则流量联系方程（1）可以简化为：

上面公式（6）中：

液压缸活塞的受力平衡方程为：

其中：

——活塞质量和负载折算到活塞上总质量；

——粘性阻尼系数：

——负载刚度：

——负载压力。

进一步的，上述的电液伺服液压缸位置反馈控制系统，为了简化控制器的设计过程，取系统的状态为：

整理（6）和（7）的公式，并考虑参数的不确定性，加入慢时变参数摄动后系统的状态方程和输出方程为：

其中，

；

；

；

；

；

。

进一步的，上述的电液伺服液压缸位置反馈控制系统，在设计控制器之前，给出下面两个假设：

假设1：干扰满足条件：

假设2：位置给定信号以下面的规律变化：

上面公式中：

——系统状态/>

——时间常数；

并且

进一步的，上述的电液伺服液压缸位置反馈控制系统，为了使得闭环系统在上面假设情况下，对给定的参数

其中，

/>

——被控制系统干扰项；

——跟踪误差；

——正常数；

——与初始条件有关的正常数。

进一步的，上述的电液伺服液压缸位置反馈控制系统，上述控制器的设计过程为：

首先，定义误差变量：

上面公式中：

——系统状态变量的期望值；

——虚拟控制量；

对公式（8）的子系统得到：

取虚拟控制量

进一步的，上述的电液伺服液压缸位置反馈控制系统，设计下面的定理：

令

。

进一步的，上述的电液伺服液压缸位置反馈控制系统，控制器中的

/>

则闭环系统的跟踪误差

上述技术方案可以看出，本发明具有如下有益效果：本发明所述的电液伺服液压缸位置反馈控制系统，通过控制过程中涉及的被控系统的二阶子系统构造一个合适的lyapunov函数，结合系统被控对象模型，通过将模型中的参数进行变量置换并选择合适的lyapunov函数，解决控制输入前含有不确定参数时所导致的控制律和自适应律产生相互包含的嵌套难题。

附图说明

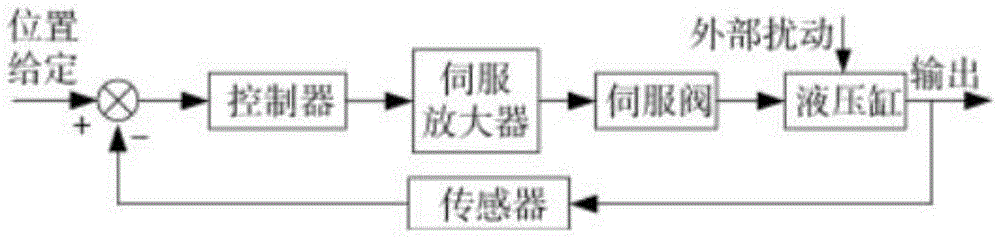
图1为本发明所述电液伺服液压缸位置反馈控制系统的系统框图；

图2为本发明所述四通阀控制液压缸的基本原理图。

具体实施方式

实施例

如图1、2所示的电液伺服液压缸位置反馈控制系统，包括控制器、伺服放大器、伺服阀、液压缸和传感器，所述控制器的信号输出端与伺服放大器连接，所述伺服放大器与伺服阀连接，所述伺服阀与液压缸的两腔体连接，并且伺服阀控制液压缸两腔体内液体的流动，所述液压缸通过传感器将位置信息反馈至控制器的信号输入端。

建立液压缸两腔体的流量连续方程为：

其中，

上面公式中各个量代表的含义为：

——液压缸无杆腔、有杆腔的压力；

——活塞位移；

——活塞运动速度；

——体积弹性模量；

——液压缸无杆腔、有杆腔的活塞面积；

——液压缸无杆腔、有杆腔的体积；

——液压缸无杆腔、有杆腔的初始容积；

——液压缸无杆腔、有杆腔的流量；

——阀芯位移；

——阀流量系数；

——伺服阀面积梯度；

——油液密度；

——供油压力和回油压力。

在液压缸两腔体的流量连续方程中，忽略液压缸两腔体的体积变化，则

根据流量-输入信号的特性曲线得到下面的公式：

其中，

上面公式中：

——伺服阀的流量-信号增益；

——面积比；

——控制输入信号；

则流量联系方程（1）可以简化为：

上面公式（6）中：

液压缸活塞的受力平衡方程为：

其中：

——活塞质量和负载折算到活塞上总质量；

——粘性阻尼系数：

——负载刚度：

——负载压力。

为了简化控制器的设计过程，取系统的状态为：

整理（6）和（7）的公式，并考虑参数的不确定性，加入慢时变参数摄动后系统的状态方程和输出方程为：

其中，

；

；

；

；/>

；

。

在设计控制器之前，给出下面两个假设：

假设1：干扰满足条件：

假设2：位置给定信号以下面的规律变化：

上面公式中：

——系统状态/>

——时间常数；

并且

为了使得闭环系统在上面假设情况下，对给定的参数

其中，

——被控制系统干扰项；

——跟踪误差；

——正常数；

——与初始条件有关的正常数。

上述控制器的设计过程为：

首先，定义误差变量：

上面公式中：

——系统状态变量的期望值；

——虚拟控制量；

对公式（8）的子系统得到：

/>

取虚拟控制量

设计下面的定理：

令

。

控制器中的

则闭环系统的跟踪误差

证明：

第一步：取lyapunov函数

对公式（15）求导得到：

对变量s求导得到：

/>

并且由s的表达式得到：

把公式（17）、（18）代入公式（16），得到

取虚拟控制量

第二步：

定义

将公式（21）求导缤结合公式（20）得到：

取自适应律为：

最后将公式（13）、（23）代入公式（22）得到：

当

由公式（25）可知，闭环系统在干扰为零时是渐近稳定的。

由公式（25）可以得到：

由于

当

公式（27）符合公式（10）的形式，可知系统满足鲁棒

以上所述仅是本发明的优选实施方式，应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以做出若干改进，这些改进也应视为本发明的保护范围。