非线性广义哈密顿系统的输入输出有限时间稳定分析方法

技术领域

本发明涉及工程技术领域，尤其涉及非线性广义哈密顿系统的输入输出有限时间稳定分析方法。

背景技术

广义系统是一类重要而广泛的动态系统，近几十年来，线性广义系统的理论日趋成熟，在稳定性和镇定性方面取得了很好的成果。由于非线性系统的复杂性，与线性广义系统相比，非线性广义系统给稳定性分析和控制设计带来了更多的挑战，因此，对非线性广义系统(NDS)的研究很少。

经检索，申请号CN106950834A的中国专利，公开了高阶非线性系统快速有限时间稳定的控制方法，其提及了高阶非线性系统中的有限时间稳定的问题；

有限时间稳定性(FTS)在文献中首次提出。它被定义为在给定的时间内在预定的边界内保持一定状态的系统。

然而，有可能约束应该应用于系统的输出而不是其状态，此外，哈密顿函数方法近年来受到了广泛的关注，如何利用哈密顿函数方法求解非线性广义系统的IO-FTS问题，实现非线性广义哈密顿系统的输入输出有限时间稳定分析方法控制，是亟需解决的问题。

发明内容

本发明的目的是为了解决现有技术中存在的缺陷，而提出的非线性广义哈密顿系统的输入输出有限时间稳定分析方法。

为了实现上述目的，本发明采用了如下技术方案：

非线性广义哈密顿系统的输入输出有限时间稳定分析方法，包括以下步骤：

S1：通过非奇异变换将NDS等效转化为非线性哈密顿微分代数系统；

S2：将Lyapunov函数转化为广义哈密顿函数，并确定上述系统在干涉函数L

S3：根据上述步骤的结果，进行仿真实验以及算例分析，分析仿真结果和控制器设计，完成对系统的有限时间稳定问题的分析。

进一步地，在步骤S1中，NDS的哈密顿形式具体为：

其中,

给出L

i)一组可积二次信号，其范数约束于张成空间[0,T]，定义为

ii)[0,T]上的一致有界信号集与集合

其中，d>0是一个实数，并且K＝B

进一步地，在步骤S2中，解决IO-FTS问题的条件为：

A1)

A2)

A3)l

A4)

A5)

其中l

进一步地，基于上述条件：

Z(x)为一个n×n的反对称矩阵，且Y(x)是一个n×n的正定矩阵，那么总会存在一个反对称矩阵Z

则能够转化广义耗散哈密顿形式，具体方式为：

因为A(x)+A(x)

其中，

当rank(E)＝r,总会存在一个正交矩阵

以此：

其中,

根据上述调价(3),系统(2)就会被等价的表达为下列形式：

其中，基于A1和A2时，系统(4)能够等价的表示为下列严格耗散形式：

其中,

进一步地，系统在干涉函数L

在A1到A5的基础上，

则系统(1)及其等价形式(5)关于

进一步地，系统在L

在A1到A5的基础上，矩阵

l

则非线性描述的哈密顿系统及其等价形式是关于

相比于现有技术，本发明的有益效果在于：

通过确定非线性哈密顿微分代数系统在干涉函数L2和L∞输入下分别满足IO-FTS的条件，并以此进行分析，并能够利用仿真结果验证哈密顿方法用于研究NDS的IO-FTS问题的有效性。

附图说明

附图用来提供对本发明的进一步理解，并且构成说明书的一部分，与本发明的实施例一起用于解释本发明，并不构成对本发明的限制。

图1为本发明实施例中在L2干扰下的系统开环曲线示意图；

图2为本发明实施例中在L2干扰下的闭环系统曲线图；

图3为本发明实施例中在L2干扰下控制信号曲线示意图；

图4为本发明实施例中在L∞干扰下的系统开环曲线示意图；

图5为本发明实施例中在L∞干扰下的系统闭环环曲线示意图；

图6为本发明实施例中在L∞干扰下控制信号曲线示意图；

图7为本发明实施例中非线性电路系统的示意图。

具体实施方式

下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。

非线性广义哈密顿系统的输入输出有限时间稳定分析方法，包括以下步骤：

S1：通过非奇异变换将NDS等效转化为非线性哈密顿微分代数系统；

S2：将Lyapunov函数转化为广义哈密顿函数，并确定上述系统在干涉函数L

S3：根据上述步骤的结果，进行仿真实验以及算例分析，分析仿真结果和控制器设计，完成对系统的有限时间稳定问题的分析。

实施例

在步骤S1中，NDS的哈密顿形式具体为：

其中,

给出L

i)一组可积二次信号，其范数约束于张成空间[0,T]，定义为

ii)[0,T]上的一致有界信号集与集合

其中，d>0是一个实数，并且K＝B

在本申请的优选实施例中，在步骤S2中，解决IO-FTS问题的条件为：

A1)

A2)

A3)l

A4)

A5)

其中l

进一步地说明：

包括以下定理：

定理2.1

给出两个实数T>0,c>0,一个矩阵Γ>0,一系列在区间[0,T]的输入信号

则系统(1)为关于

基于上述条件，Z(x)为一个n×n的反对称矩阵，且Y(x)是一个n×n的正定矩阵，那么总会存在一个反对称矩阵Z

则能够转化广义耗散哈密顿形式，具体方式为：

因为A(x)+A(x)

其中，

当rank(E)＝r,总会存在一个正交矩阵

以此：

其中,

根据上述调价(3),系统(2)就会被等价的表达为下列形式：

其中，基于A1和A2时，系统(4)能够等价的表示为下列严格耗散形式：

其中,

其中，2.1.Y(x)>0是

为了更好的理解技术方案，证明方式如下：

根据引理2.1和

那么

可以得到

同时，还可得到：

这就证明了B

在本申请的具体实施例中：

系统在干涉函数L

在A1到A5的基础上，

则系统(1)及其等价形式(5)关于

系统在L

在A1到A5的基础上，矩阵

l

则非线性描述的哈密顿系统及其等价形式是关于

需要进一步说明的是，对获得结果证明的方式具体为：

因为系统(1)没有脉冲，所以选择广义Lyapunov函数

则V(x)的导数为:

由(6)可知

同时将(7)从0到t≤T.两边积分，此外，需要注意的是w(·)属于

基于A2 A3,A4,并且d≤c,我们得到：

所以,y(t)

为了更好的理解本申请的技术方案，以下结合仿真算例和实验进一步说明。

定理2.2：如果假设A1到A5都成立，矩阵

l

则非线性描述的哈密顿系统(1)及其等价形式(5)是关于

证明:从引理2.2，我们知道系统(1)没有脉冲，根据定理2.2中证明的不等式(7)。很明显

考虑Ex(0)＝0并且将(9)在t∈[0,T]内积分。我们得到

根据条件(8)，可以得出：

因此,y(t)

进一步地

广义哈密顿系统有限时间输入输出的镇定分析：

NDSs具体为：

其中,A(x),B,C,E.w和系统(1)一样，

并记：

为了探讨控制问题，我们加入以下假设：

A(3.1)

A(3.2)

A(3.3)假设总存在一个在平衡点

如果A(3.2)和A(3.3)成立，系统(10)在平衡点是指数为1，则系统(10)为脉冲能控，,我们可以设计控制器为：

假设A(3.1)成立，基于前面的转化过程我们可以得到最终的严格耗散形式：

定理3.1假设A(3.1)成立，如果矩阵

使得

那么系统(10)就是IO-FTS的。

证明：过程与前面一致。

更近一步地

仿真实验：

选择非线性电路系统，具体如图7所示；

在该非线性电路系统中，电容是由电荷控制的，而电感是由磁通链w控制的；它们的特性可以分别表示为u

根据Kirchhoff电流定律和Kirchhof电压定律，该系统可表示为

令

记

则系统(11)可表述：

选取Hamilton函数

且A(x)+A

经检验A(1)和A(2)都成立，我们可以设正交矩阵M为

所以系统(13)可以表示为以下微分代数形式

其中，

设计以下控制律：

令

则：

可见满足定理3.1，所以所举实例系统(12)就是IO-FTS的。

为了更进一步的理解，以下结合仿真图进行阐述。

仿真图：根据以下参数：

Γ＝I

在l

给出两类干扰信号：

w(t)＝cos(-0.1t)∈L

在干扰为

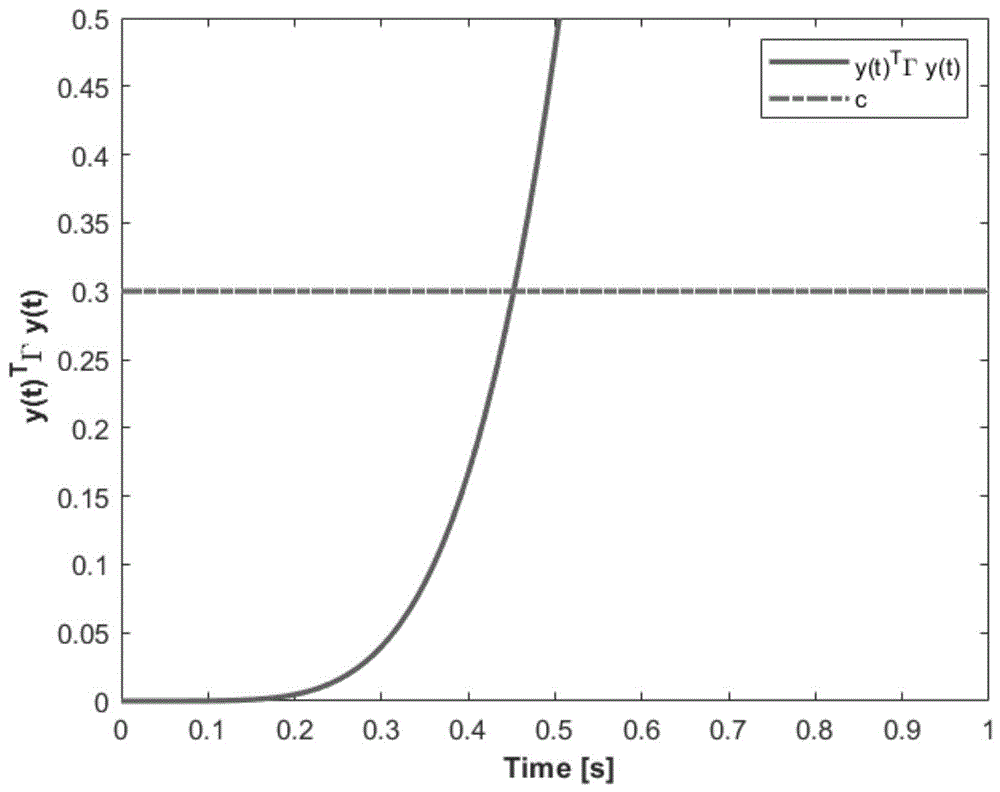
由图1可以看出，在没有加控制器的情况下，在有限时间1秒内，系统y(t)

由图2可以看出，加了控制器之后闭环系统的y(t)

由图3可以看出，因为所给有限时间T＝1,之前的L1和L2参数不变，所以L1＞TL2.满足定理2.2，下面便可以开始在L∞干扰下的仿真实验。此时干扰信号为w(t)＝cos(-0.1t)∈L

由图4可以看出在没有加控制器的情况下，系统y(t)

由图5-6可以看出，加了控制器之后，有限时间内闭环系统的y(t)

以上所述，仅为本发明较佳的具体实施方式，但本发明的保护范围并不局限于此，任何熟悉本技术领域的技术人员在本发明揭露的技术范围内，根据本发明的技术方案及其发明构思加以等同替换或改变，都应涵盖在本发明的保护范围之内。